Spatiotemporal Multi-Graph Convolution Network for Ride-hailing Demand Forecasting

    今天实验室分享了一篇2019年AAAI的论文：Spatiotemporal Multi-Graph Convolution Network for Ride-hailing Demand。讲的是通过时空多图卷积来进行打车需求的预测。

• 1. 任务
• 2. 数据处理
  • 2.1. Neighborhood
  • 2.2. Functional similarity
  • 2.3. Transportation connectivity
• 3. ST-MGCN模型
  • 3.1. Temporal correlation modeling
  • 3.2. Multi-Graph Convolution

    上学期实验室也分享论文，但是分享之后就忘了。所以决定从这学期开始，对一些我觉得对我有帮助的论文记录下来

    这篇论文和以前读到的图卷积的论文的不同是：这篇论文构建了多个图。
    在介绍这篇论文之前，先写出自己以前一直没有弄清楚的一个点。一个图有2个矩阵，一个是邻接矩阵A，一个是图信号矩阵X。邻接矩阵A表示的是这个图的结构，节点与节点之间的连接关系。图信号矩阵表示这个图中每个节点的特征。假设一个图有100个节点，每个节点有3个特征，那么邻接矩阵A的维度是100x100，图信号矩阵X的维度是100x3。在构造下面的3个不同的图时，只是邻接矩阵A不同，图信号矩阵都是一样的。在计算图卷积的时候会同时用到图的邻接矩阵和图信号矩阵。

1. 任务

    这篇论文的任务就是一个区域$T$个时间段的特征(可能有1个特征即打车订单数，也可有多个特征)预测第$T+1$时刻的特征值。

2. 数据处理

    首先这篇论文将一个城市进行网格划分，一个网格表示一个区域region。然后对这些网格构建图。多图就体现在构建图上，原先的论文是构建一个图，这篇论文构建了3个图。论文的任务是打车需求量预测。论文中说一个region的打车需求可能和以下3个方面有关系：邻近区域neighborhood，和该区域功能相近的区域，和该区域道路可达的区域。所以论文根据以上3种关系分别构建了3个图。

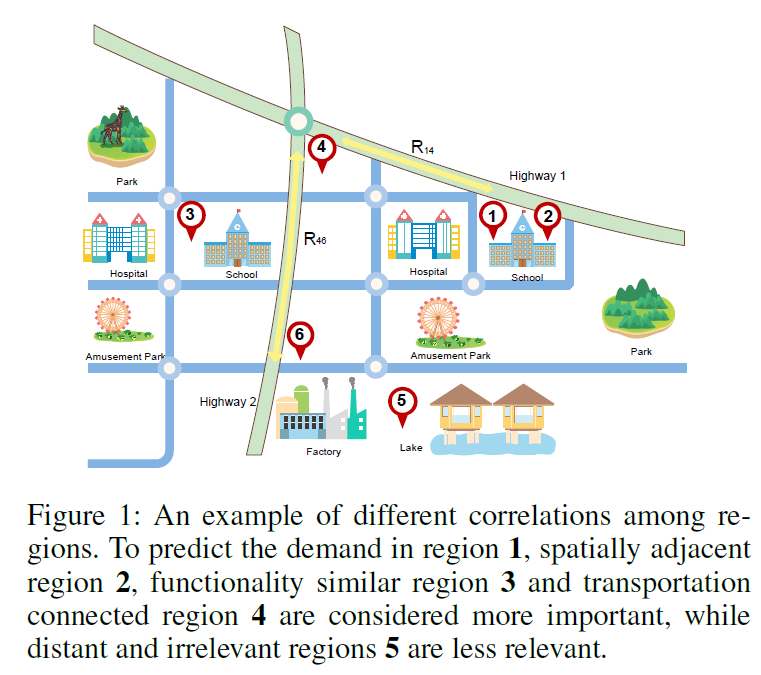
    例如上图所示，和region1相邻的区域是region2，和region1功能相似的是region3，和region1交通可达的是region4。

2.1. Neighborhood

    构建的邻居图用$\mathcal{G}_N=(V,A_N)$表示，其中V表示所有的区域，$A_N$表示区域与区域之间的邻居关系。构建的图一个节点表示一个region，2个区域有边表示这2个区域是邻居，没有边相连表示不是邻居。这样就可以从原始的图中根据邻近关系构建出一张图

    怎么判断两个区域是否相邻？首先把一个city划分成grid，一个区域周围的8个区域就是这个区域相邻，那么$A_{N,ij}=1$,否则为0。这样就构建了一个大小为$\mathbb{R}^{|V|\times|V|}$的矩阵$A$。

2.2. Functional similarity

    构建的功能相似图用$\mathcal{G}_N=(V,A_S)$表示，其中V表示所有的区域，$A_S$表示区域与区域之间的功能相似关系。构建的图一个节点表示一个region，2个区域有边表示这2个区域之间的相似关系，是一个[0,1]之间的数。计算两个区域之间的相似关系：首先需要知道每个区域的POI向量。POI向量是这个区域在某个类别的POI的个数，例如POI有5类，分别是：学校、公园、医院、商场、居民区，这种区域有1个学校，2个公园、0个医院、3个商场、1个居民区，则POI向量为[1,2,0,3,1]，计算两个region的功能相似性即计算两个POI向量的相似性。

2.3. Transportation connectivity

    构建的交通可达图用$\mathcal{G}_N=(V,A_C)$表示，其中V表示所有的区域，$A_C$表示区域与区域之间的可达关系。构建的图一个节点表示一个region，2个区域可达判断的依据是通过OpenStreetMap，看两个区域之间是否有highway，subway，motorway，如果有的话就表示这两个区域交通可达。如果两个
region交通可达，则conn($v_i,v_j$)=1,否则为0。然后需要注意的是这里减去了邻居关系。因为考虑了交通可达，不想再次考虑邻居关系。取max为了保证没有负值。

3. ST-MGCN模型

    这篇论文提出的模型是$spatiotemporal \quad multi-graph \quad convolution \quad network\quad(ST-MGCN)$。首先输入是原始数据，一个城市所有区域的特征，不同的层表示不同的时间，那么输入$X\in\mathbb{R}^{T\times|V|\times{P}}$，每一个时刻有一个图信号矩阵，维度为$|V|\times{P}$，一共有$T$个时刻。然后从原始数据中提取出3张图，分别表示region之间的邻居图、功能相似图、交通可达图。这三张图的维度也是$\mathbb{R}^{T\times|V|\times{P}}$，只是这3张图的邻接矩阵不同。然后经过$contextual \quad gated \quad recurrent \quad neural\quad nwtwork\quad (CGRNN)$对时间进行建模，然后分别输出一张图，一共输出3张图。然后再用multi-graph convolution对空间进行建模，最终输出一张图，表示下一时刻各个节点的特征

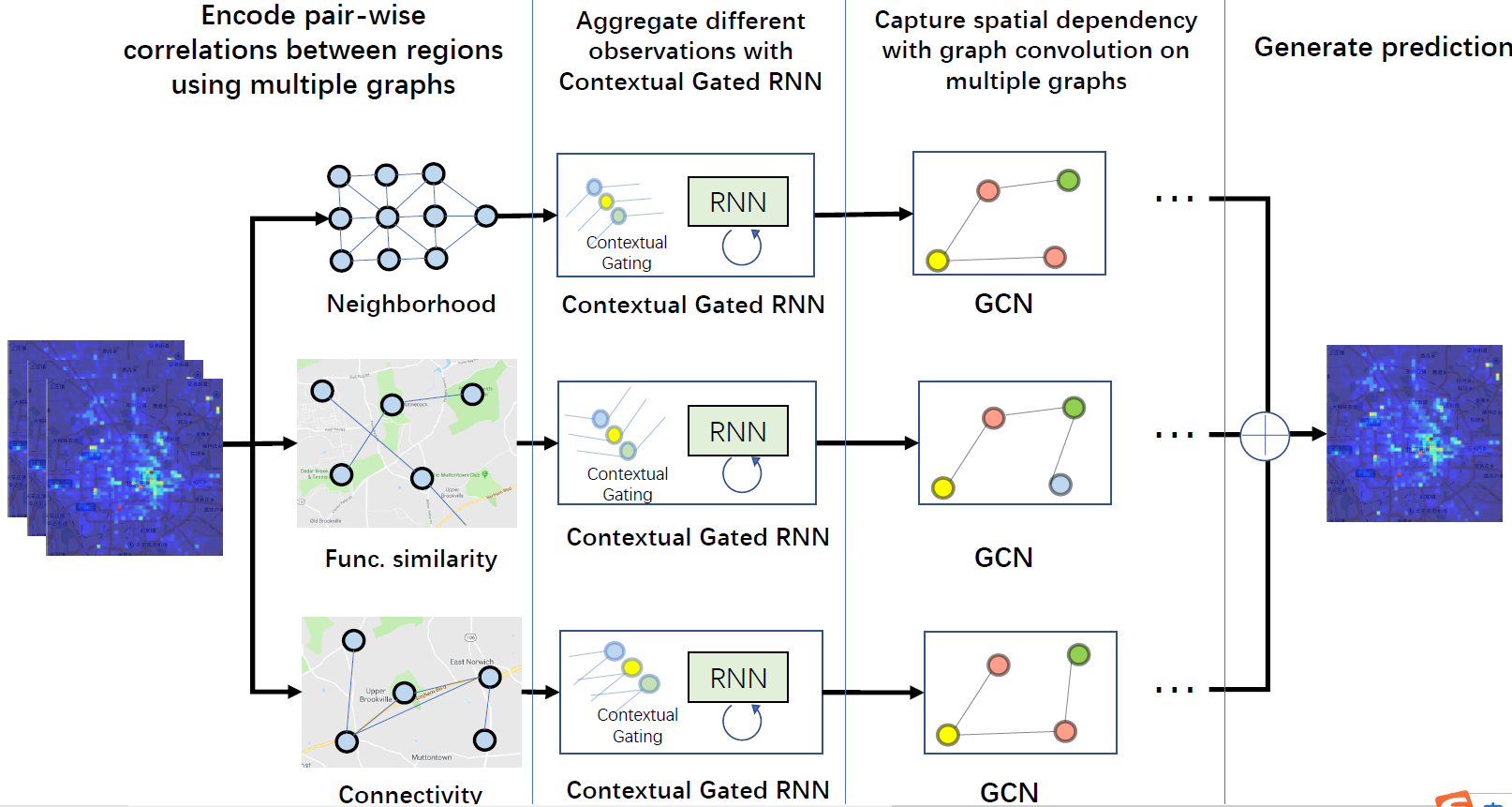
3.1. Temporal correlation modeling

    提出$Contextual \quad Gated \quad Recurrent \quad Neural \quad Network \quad (CGRNN)$来对不同时刻的图信号进行建模。在一个城市的打车需求，在某一个时刻，可以记录每个节点(region)的特征，因为是时间序列数据，就有了时间的维度，这样就可以形成T个图信号。CGRNN在对时间建模时引入了上下文信息contextual information。其中contextual information指的是邻近区域的信息，通过图卷积GCN来获取。模型框架图如下所示：

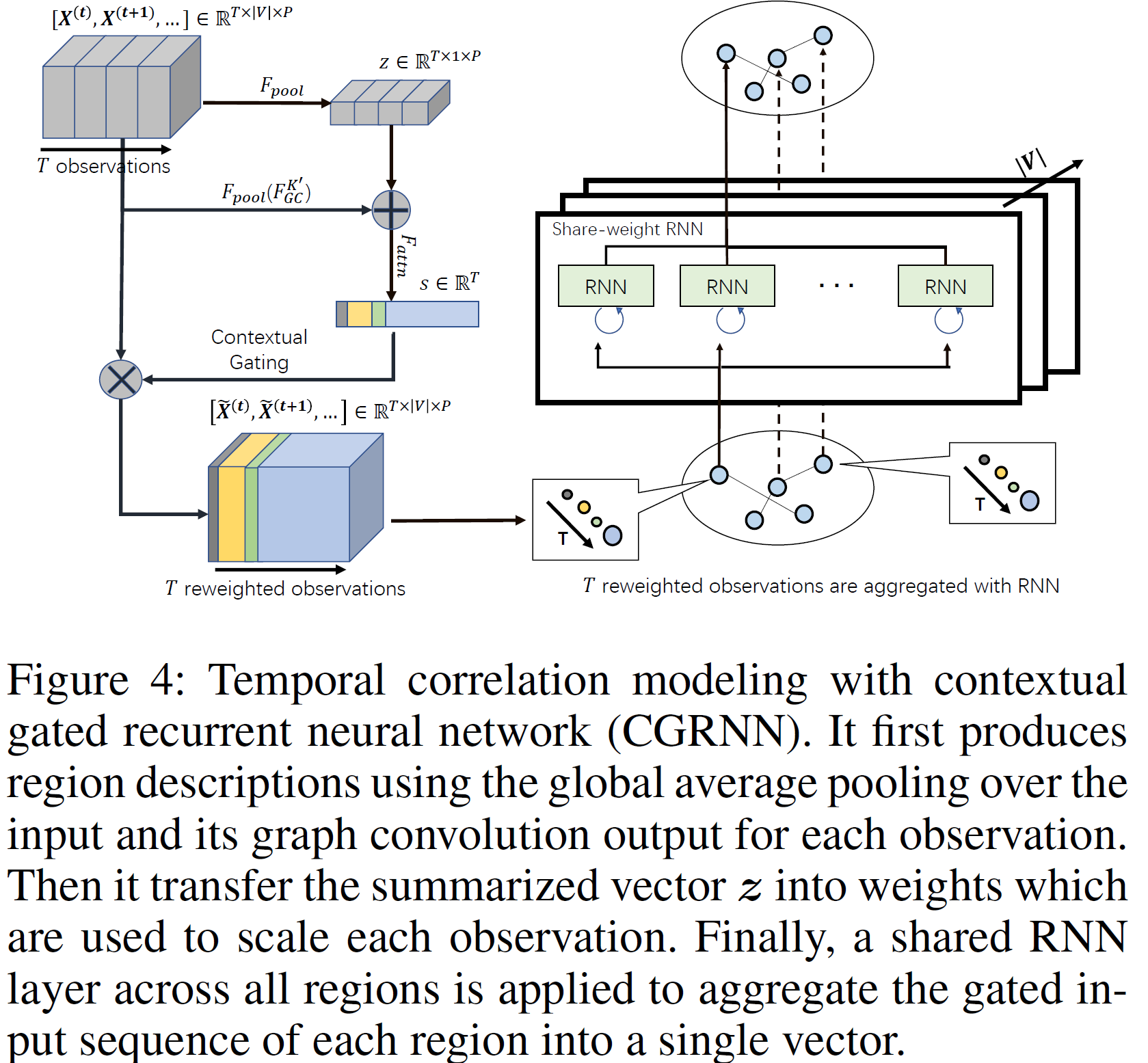
    有T个时刻，第$t$个时刻的观察值是$X^{(t)}\in\mathbb{R}^{|V|\times{P}}$，其中$P$表示每个节点的特征维度，如果$P=1$表示只有一个特征，仅包含region的打车订单数。

    按照上面的模型图，执行的顺序是：
（1）先把原始的图$[X^{(t)},X^{(t+1)},…]\in\mathbb{R}^{T\times|V|\times{P}}$经过一个池化层，把一个特征在所有区域的特征值取平均，这样就变成维度为$\mathbb{R}^{T\times1\times{P}}$，与此同时对原始的图信号$[X^{(t)},X^{(t+1)},…]\in\mathbb{R}^{T\times|V|\times{P}}$中的每个时刻的图信号$\mathbb{R}^{|V|\times{P}}$进行卷积操作，K=K‘，表示得到一个结合K`阶邻居信息图$\mathbb{R}^{|V|\times{P}}$，T个时刻共得到T个$\mathbb{R}^{|V|\times{P}}$,即$\mathbb{R}^{T\times|V|\times{P}}$，再经过一个池化操作，得到一个$\mathbb{R}^{T\times1\times{P}}$，然后把2个$\mathbb{R}^{T\times1\times{P}}$进行拼接concatenate，得到一个$\mathbb{R}^{T\times1\times{2P}}$，每个region的特征维度变成2P，前一个P表示的是自己的特征，后一个P表示的整合邻居后的特征。
上述的操作在论文中的式子如下：

$$\hat{X}^{(t)}=[X^{(t)},F_\mathcal{G}^{K`}(X^{(t)})] \quad for \quad t=1,2,...T \tag{6}$$ $$\mathcal{z}^{(t)}=F_{pool}(\hat{X}^{(t)})=\frac{1}{|V|}\sum_{i=1}^{|V|}\hat{X}_{i,;}^{(t)} \quad for \quad t=1,2...T \tag{7}$$

论文中的式子是先拼接成$\mathbb{R}^{T\times|V|\times{2P}}$，然后再池化成$\mathbb{R}^{T\times1\times{2P}}$，但是模型图上是先分别池化成$\mathbb{R}^{T\times1\times{P}}$，再拼接成$\mathbb{R}^{T\times1\times{2P}}$
（2）然后经过2个全连接层，得到关于时间的attention,s的维度是$s\in\mathbb{R}^T$

$$s=\sigma(W_2\delta(W_1\mathcal{z}))\tag{8}$$

（3）将s和原始图信号进行内积，得到缩放后的图信号，维度为$\mathbb{R}^{T\times|V|\times{P}}$。

$$\widetilde{X}^{(t)}=X^{(t)}\circ s^{(t)} \quad for\quad t=1,2...T\tag{9}$$

（4）最后经过一个共享的RNN神经网络。对于每一个节点，在每一个时刻会有一个P个特征值，经过T个时刻，会形成一个$\mathbb{R}^{T\times{P}}$的矩阵，一共有V个节点，对每一个节点的时间序列都应用这个RNN，最后每个节点都会输出一个隐藏变量$H_i$,V个节点会形成V个隐藏变量，最终会输出一个$\mathbb{R}^{|V|\times{P}}$的矩阵。

$$H_{i,:}=RNN(\widetilde{X}_{i,:}^{(1)},...,\widetilde{X}_{i,:}^{(T)};W_3) \quad for \quad i=1,2...|V|\tag{10}$$

    一共有三个图，所以经过CGRNN会输出3个$\mathbb{R}^{|V|\times{P}}$的矩阵,这时的邻接矩阵还是输入图的A。

3.2. Multi-Graph Convolution

    对时间建模完成之后，接下来使用Multi-graph Convolution对空间进行建模。

$$X_{l+1}=\sigma(\bigsqcup_{A\in\mathbb{A}}f(A;\theta_i)X_lW_l)$$

其中$\bigsqcup$是聚合函数，可以是sum，avg，max等，其中$f(A;\theta_i)$是ChebNet卷积核，是$\sum_{k=0}^K\theta_kL^k$,卷积运算可以写成$g_{\theta}*x=(\sum_{k=0}^K\theta_kL^k)x$，其中$L_{ij}^k=0$表示节点$i$到节点$j$可以在k跳到达，$k$定义了图卷积的感受野。以road connectivity为例，$\mathcal{G}_C=(V,A_C)$中，拉普拉斯矩阵L由邻接矩阵A计算得到，在道路连通图中的邻接矩阵$A_{C,1,4}=1;A_{C,1,6}=0;A_{C,4,6}=1$表示region1和4道路连通，region1和6道路不连通，region4和6道路连通。拉普拉斯矩阵L中，对角线表示这个节点的度，其余值不为0表示这个节点的一阶邻居，道路连通图的拉普拉斯矩阵$L_{C,1,4}^1\ne0;L_{C,1,6}^1=0;L_{C,4,6}^1\ne0$。如果在ChebNet中K=1，则对于region1这个节点来说，经过一次卷积运算后，下一层的输出region1这个节点新的特征中只包含了region1的一阶邻居的信息，不包含region6的信息，因为$L_{C,1,4}^1\ne0;L_{C,1,6}^1=0$，如果ChebNet中的K=2，则region1经过一次图卷积运算，下一层region1的特征包含一阶邻居region4和二阶邻居region6的信息，因为$L_{C,1,4}^2\ne0;L_{C,1,6}^2\ne0$。

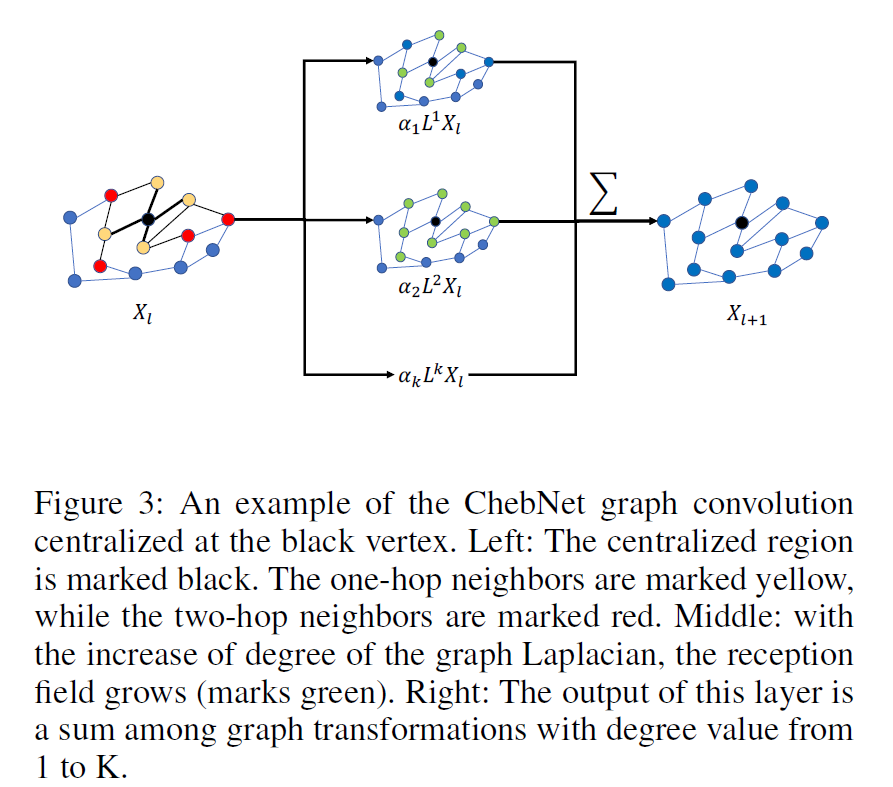
    这个图中，假设ChebNet的$K=k$,根据卷积的运算公式$g_{\theta}*x=(\sum_{k=0}^K\theta_kL^k)x$，对于上图中，把黑色的点当做中心结点，黄色的点是一阶邻居，红色的点是二阶邻居。蓝色的点是三阶邻居。首先计算$k=1$时，则对于黑色的中心结点，整合了一阶邻居的信息得到一个图信息矩阵。然后计算$k=2$时，则对于黑色的中心结点，结合一阶邻居和二阶邻居的信息得到一个新的图信号矩阵，一直到$K=k$，得到了$k$个图信号矩阵，然后把这$k$个图信号矩阵相加得到下一层黑色的中心结点的表示。如果对$X_l$中的每个节点都执行这样的操作，则经过图卷积，下一层的输出$X_{l+1}$则表示每个节点整合了邻居信息得到的一个新的图信号矩阵
     这样每一个图经过一个图卷积得到一个新的图信号矩阵，3个图得到3个新的图信号矩阵，然后再执行$\bigsqcup$聚合操作，在这篇论文中，$\bigsqcup$选择的是sum操作，就是说得到的3个新的图信号矩阵，直接相加就得到一个图，表示最终的预测结果。