Yehuda Koren发表在2008KDD上的一篇论文。他也是Netflix Prize的冠军队成员，是推荐系统领域的大神级人物。他带领的团队在 Netflix Prize 比赛中拿到过两次进步奖（progress award），参与的团队拿到过 2009 年 Netflix Prize 比赛的百万美金大奖。当年比赛的题目是 netflix 电影评分预测，Yehuda Koren 所在团队提出的算法在测试集上的均方根误差为 0.8567，比比赛开始时的最高成绩提高了 10.06%。Yehuda Koren 等人当年做出的算法是基于矩阵分解的算法，优于传统的最近邻基础，已经成为现在几乎所有推荐系统的基础。

1. 引言

实现协同过滤CF的2个比较成功的方法：邻居模型（user-based和item-based）和潜在因子模型，本篇论文对以上两种方法进行融合。

邻居方法是计算item或user的相似性。

潜在因子模型，例如奇异值分解(SVD)，使用多个因素来表示item

这篇文章首次提出将邻居方法和潜在因子模型进行融合。

作者发现整合不同形式的输入到模型中是非常重要的，传统的方法一般输入的都是高质量的显示反馈，例如user-item评分矩阵，然后显示反馈有时无法获取到，一些隐式信息也能反映用户的喜好，隐式信息包括：购买历史，浏览记录，搜索模式，甚至鼠标移动。在本篇模型中，融合显示和隐式信息。

2. 定义

用户$u,v$
物品$i,j$
评分$r_{ui}$，所有的评分$\mathcal
{K}=\{(u,i)|r_{ui}已知\}$
需要预测的值$\hat{r_{ui}}$

在评分矩阵中，大部分的值缺失，为了避免过度拟合稀疏的数据，添加正则化

2.1. baseline

普通的协同过滤方法CF，$b_{ui}$是基准推荐模型给出的评分：

$b_{ui}=\mu + b_u + b_i$

其中$\mu$表示所有物品的平均评分，$b_u$表示用户$u$评分的偏差，$b_i$表示物品$i$评分的偏差。假设要对电影《泰坦尼克号》评分，所有电影的评分$\mu=3.7$，天威这个电影比较好，评分比一般的电影高$b_i=0.5$分，而用户$u$在电影上比较挑剔，评分比一般评分低$b_u=0.3$分，则《泰坦尼克号》的评分为$3.7-0.3+0.5=3.9$分。

为了求$b_i,b_u$，使用下面的目标函数

$\mathop{min} \limits_{b*} \sum_{(u,i) \in \mathcal{K}} (r_{ui}-\mu-b_i-b_u)^2+\lambda_1(\sum_\mu b_u^2 + \sum_{i}b_i^2)$

2.2. 邻居方法

基于邻居方法来实现协同过滤CF。先出现基于用户的CF，后提出基于物品的CF。在预测中，面向物品的CF更容易解释，因为我们更容易解释物品之间的相似性，而用户之间的相似性不容易解释。下面以面向物品的CF为例。

面向物品的CF核心是计算相似性。可以使用皮尔森系数，但由于评分矩阵非常系数，可以对皮尔森系数进行修正：

$s_{ij}=\frac{n_{ij}}{n_{ij}+\lambda_2}\rho_{ij}$

其中$n_{ij}$表示同时给物品$i,j$都进行评分的用户个数，$\lambda_2$通常为100

为了求出用户$u$对未见过的物品$i$的评分$r_{ui}$，首先从用户$u$已经评分过的物品中找出与物品$i$最相似的$k$个物品，表示为$S^k(i;u)$，被预测的值$\hat{r}_{ui}$为这$k$个物品评分的加权平均

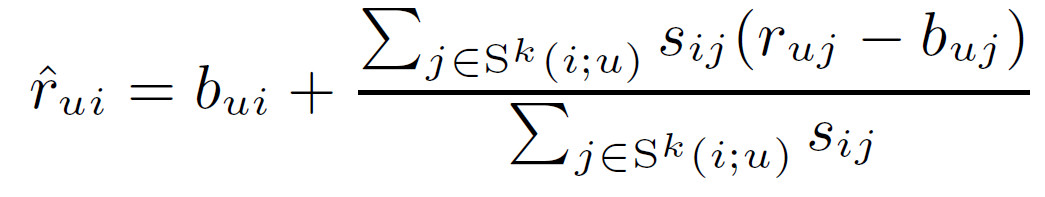(3)

但是这种方法不能通过正式模型来证明，此外该相似性度量没有分析所有邻居间的相互作用，而权重和为1的事实导致该方法完全依赖邻居，即使在没有邻居的情况下。

为了解决以上问题，本文提出新的插值权重$\theta^u_{ij}$

$\hat{r}_{ui}=b_{ui}+\sum_{j \in S^k(i;u)}\theta^u_{ij}(r_{uj}-b_{uj})\quad \quad (4)$

至于$\theta^u_{ij}$怎么得到的，参考《Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights》

2.3. 潜在因子模型

潜在因子模型感觉就是矩阵分解MF，通常可以使用奇异值分解来实现，使用向量$p_u \in \mathbb{R}^f$表示用户$u$，使用向量$q_i \in \mathbb{R}^f$表示物品$i$。通过$\hat{r}_{ui}=b_{ui}+p_u^Tq_i$来进行预测。

在信息检索中，通常使用SVD进行矩阵分解，然而评分矩阵中通常比较稀疏，会造成过拟合的问题。早期的方法通过插值的方法来构造稠密矩阵，但这种代价太大。因此最近的额工作通常直接对评分矩阵进行建模，采用正则化来避免过拟合。

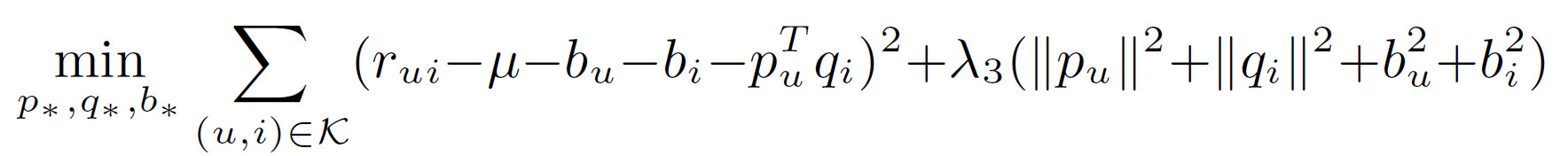
Paterek提出使用NSVD，这种方法避免显式参数化每个用户，而是根据用户评价的物品对用户进行建模。对于每个物品，使用2个向量表示$q_i,x_i$，根据用户所评价的物品来表示用户向量，其中$R(u)$是用户评价的物品集合，用户向量为$(\sum_{j \in R(u)}x_j)/\sqrt{|R(u)|}$，最终的预测评分：

$\hat{r}_{ui}=b_{ui}+q_i^T (\sum_{j \in R(u)}x_j)/\sqrt{|R(u)|}$

本篇论文在此基础上进行扩展。

2.4. Netflix数据集

使用Netfix电影评分数据，评价指标

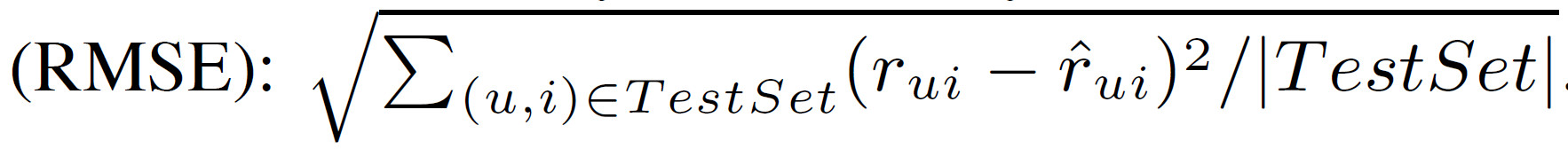
测试集中包含140万个最新电影评分，这里面包含较多的对电影评分不多的用户，很难预测，更符合实际情况。

Netflix数据集是现在Netflix Prize竞赛使用的数据集，该竞赛的基准是Netflix的专有系统，测试集的RMSE为0.9514，大奖将办法给将RMSE降低至0.8563以下(提升10%)的团队。本篇论文的RMSE为0.887

2.5. 隐式反馈

像Netflix这样的数据，隐式数据是用户的电影租赁记录，并不需要用户显示的评分，但是这样的数据并不能获取到，现在所能获取到的数据就是显示评分数据。

在本篇模型中，不限制使用隐式数据的类型，每个用户有2个向量表示，一个显式数据$R(u)$，例如用户$u$所评分的物品；一个隐式数据$N(u)$

3. 邻居模型

在本篇论文中，我们引入了新的邻居模型，该模型不仅提升了准确率，并且整合了隐式信息。

之前的模型使用$\theta^u_{ij}$或$\frac{s_{ij}}{\sum_{j \in S^k(i;u)}s_{ij}}$将物品$i$和它的邻居$S^k(i;u)$联系起来.

为了促进全局优化，我们抛弃特定用户的权重，使用全局权重，该权重独立于特定的用户。从物品$j$到物品$i$的权重表示为$w_{ij}$，该权重通过优化学习得到，预测得分$\hat{r}_{ui}$公式如下：

$\hat{r}_{ui} = b_{ui}+\sum_{j \in R(u)}(r_{uj}-b_{uj})w_{ij} \quad \quad (6)$

我们提出的公式6和公式4不同，公式6中的$w_{ij}$不是针对特定用户的。$R(u)$是用户评价的物品集合。公式6是对$R(u)$求和，公式4是对$S^k(i;u)$求和。用户$u$已经评分过的物品中找出与物品$i$最相似的$k$个物品，表示为$S^k(i;u)$

在邻居模型中，权重通常表示未知物品和已知物品的插值系数，也表示和baseline评估分数的偏差。残差$r_{uj}-b_{uj}$和这些偏差$w_{ij}$相乘。对于2个相关的物品$i,j$，希望$w_{ij}$越大越好。如果用户$u$对物品$j$评分高于期望值$(r_{uj}-b_{uj})$时，我们也希望增加用户$u$对物品$i$的评分，通过加上$(r_{uj}-b_{uj})\times w_{ij}$。我们的评估不会和baseline差太多。主要有以下2个原因：(1)如果用户$u$对物品$j$的评分和期望值差不不大，则$r_{uj}-b_{uj}$基本为0。(2)如果物品$j$对物品$i$来说是未知的，则$w_{ij}$基本为0。通过这种考虑对公式(6)进行改进。首先我们使用隐式反馈，通过这可学习用户偏好。最终，我们在后面添加一组权重来重写公式(6)

$\hat{r}_{ui} = b_{ui}+\sum_{j \in R(u)}(r_{uj}-b_{uj})w_{ij}+\sum_{j \in N(u)}c_{ij} \quad \quad (7)$

$c_{ij}$和$w_{ij}$都是权重，对于物品$i$和物品$j$，用户$u$对物品$j$的隐式偏好会主导用户修改对物品$i$的评分$r_{ui}$,通过加上偏差$c_{ij}$。

上式中的权重是全局的偏差，而不是针对某个特定用户，这种方式强调了缺失值的影响。换句话说，用户的偏好不仅仅取决于他的评分，还取决于他没有评分的东西。例如要预测用户对“指环王3”的评分，如果用户对“指环王1和2”评分也比较高，则从指环王1和2到指环王3的权重就比较大，但是如果用户没有对指环王1和2进行评分，则对指环王3进行评分时，就需要进行惩罚。

下面给出更一般的公式

$\hat{r}_{ui} = \mu + b_i + b_u + \sum_{j \in R(u)}(r_{uj}-b_{uj})w_{ij}+\sum_{j \in N(u)}c_{ij} \quad \quad (7)$

其中$\mu + b_i + b_u$是其他模型的预测值。

当前的方案中，对那些评分数据较多(具有高的$|R(u)|$)或隐式数据较多(具有高的$N(u)$)的的用户，鼓励生成较大偏差的评分结果，与baseline相比。也就是说对于那些输入数据较多的用户，我们更愿意预测更奇怪和不太常见的建议，对于那些少量输入数据的用户更希望给出接近baseline的估计值。但是，根据我们的经验可知，当前的模型在某种程度上过分强调了较多评分者和较少评分者之间的二分法，为了缓和这种情况，将预测规则修改如下：

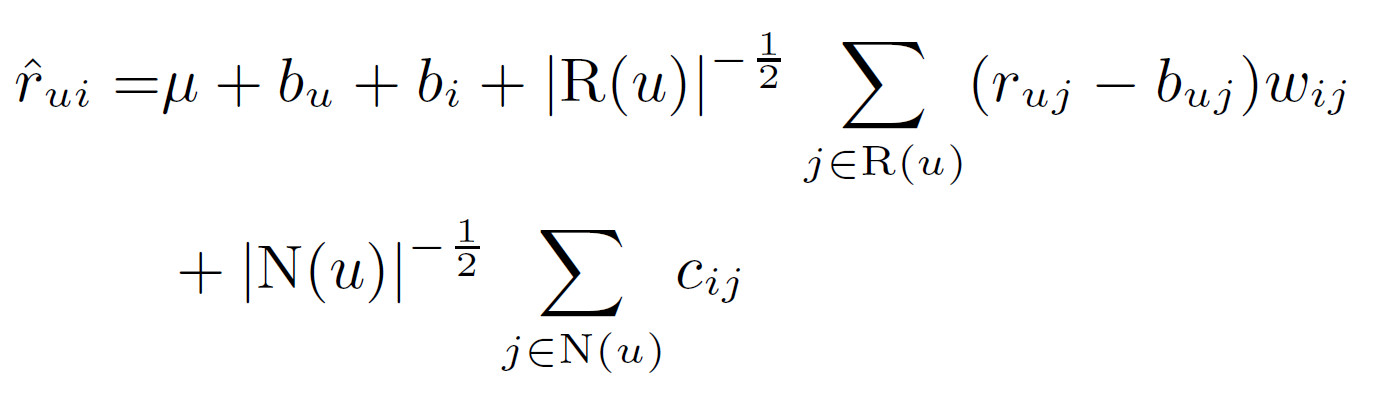
可以通过修剪与不太相关的项目来减少参数，使用$R^k(i;u)$表示在用户$u$评价的物品中，与物品$i$最相似的$k$个物品。$N^k(i;u)$表示在用户$u$隐式偏好的物品中，与物品$i$最相似的$k$个物品

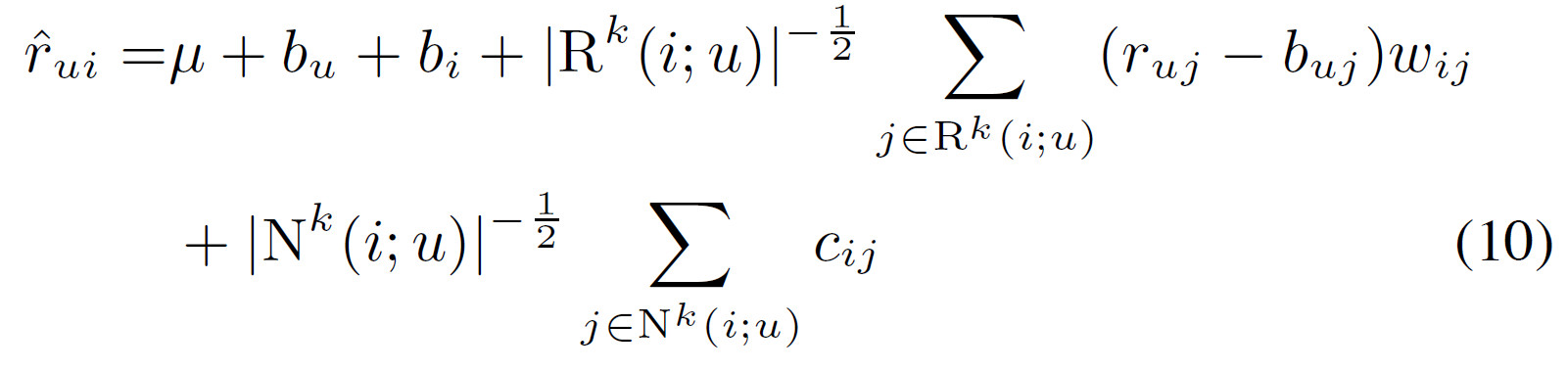
下面是我们提出方案的最终版，新的邻居模型的主要目标是利用有效的全局优化过程。在下面的优化过程中，加上正则项。

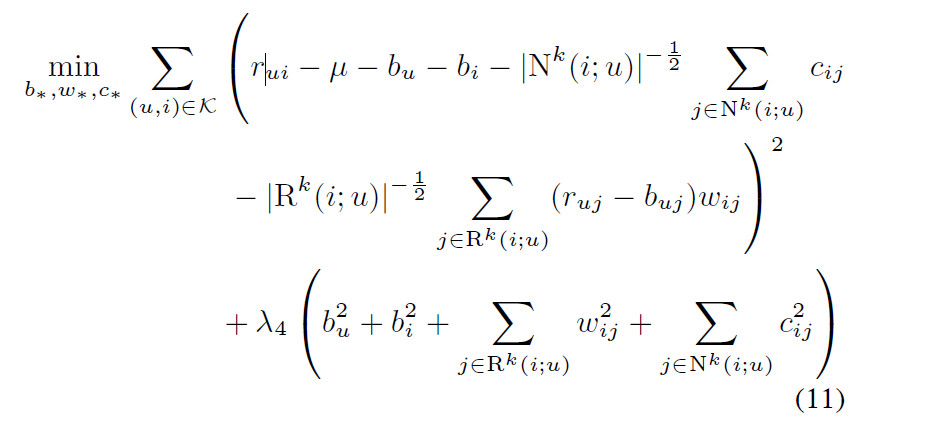
4. 隐式因子模型

隐式因子模型中较流行的是SVD，对评分矩阵进行分解，每个用户$u$使用向量$p_u \in \mathbb{R}^f$表示，每个物品$i$使用向量$q_i \in \mathbb{R}^f$，通过下式得到预测结果：

$\hat{r}_{ui}=b_{ui}+p^T_uq_i \quad \quad (12)$

通过下面的公式进行优化求解：

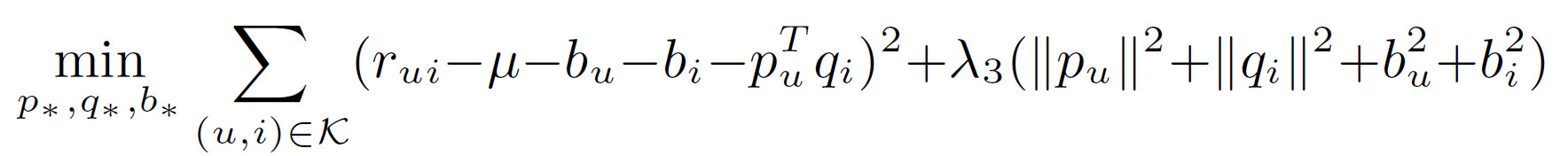
下面我们通过添加隐式信息对SVD进行扩展，预测公式如下所示：

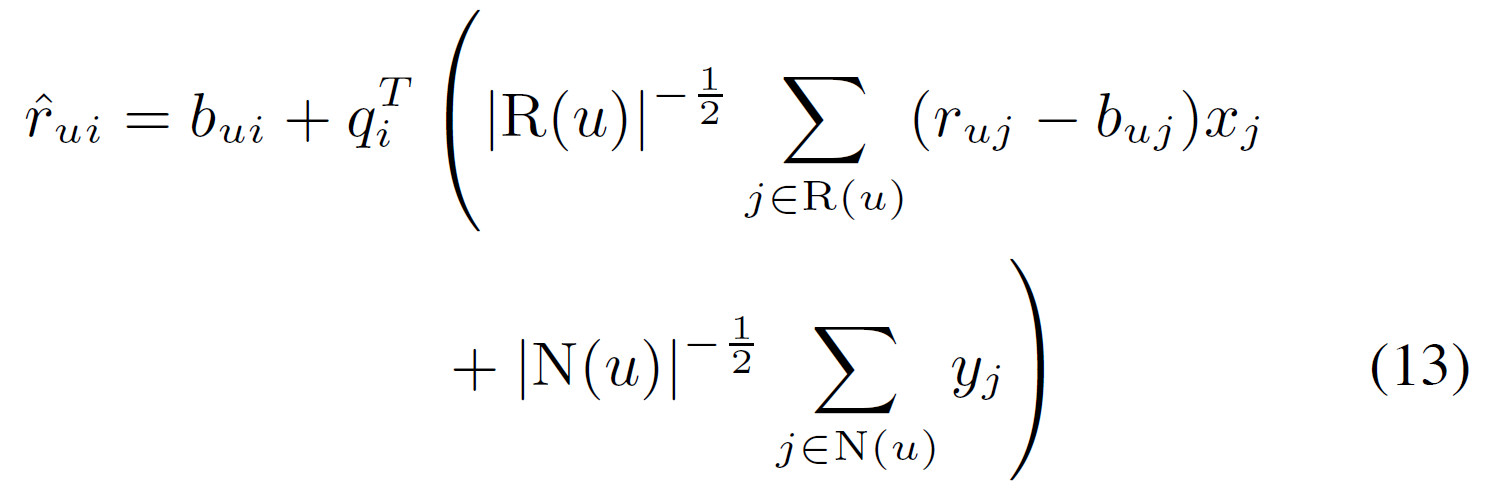
在上式中，每个物品$i$都有3个向量$q_i,x_i,y_i \in \mathbb{R}^f$。在这里我们并没有对用户$u$给出一个显示的向量表示，而是使用该用户过去评分的商品来表示用户$u$的喜好。使用下面的公式代替用户向量$p_i$

$|R(u)^{-\frac{1}{2}}|\sum_{j \in R(u)}(r_{uj}-b_{uj})x_j+|N(u)|^{-\frac{1}{2}}\sum_{j \in N(u)}y_j$

带有正则项的损失函数就变成：

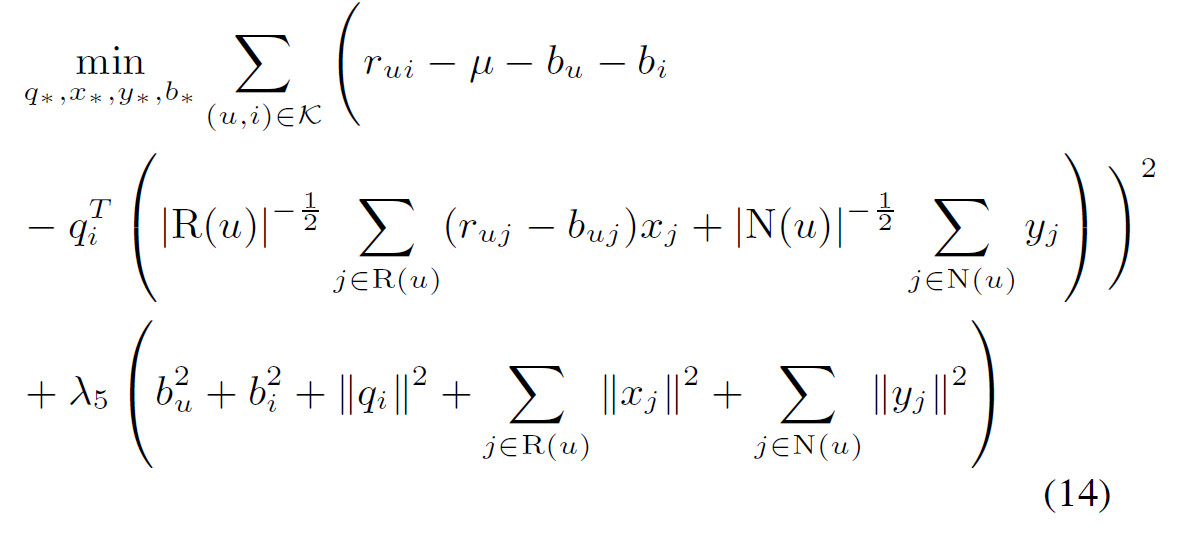
本文提出的SVD被称为“非对称SVD”，主要有以下优点：

更少的参数。通常用户的数量远大于商品的数量。因此使用物品参数代替用户参数降低模型复杂度
冷启动问题。因为非对称SVD中没有用户参数，只要用户在系统中有反馈，我们就可以处理新用户问题，并不需要重新训练模型。需要注意的是对于新的物品，我们需要学习新的参数。换句话说：系统对于新用户可以给出即时的推荐，对于新物品的推荐，需要等待一些时间。
可解释性。以前的SVD是通过对用户过去的行为进行抽象，抽象为用户向量，无法直接解释哪个历史行为对当前的预测结果更重要。非对称SVD算法没有对用户进行超互相，最终的预测结果是用户历史反馈的直接函数，所以可以直观的看出历史哪个行为对当前预测更重要，解释性更强。面向物品的协同过滤也有这个优点。
有效地整合隐式反馈。隐式反馈提供了额外的用户爱好，可能提升推荐准确率。在公式(13)中，当$|N(u)|$变大时，隐式反馈更重要。当$R(u)$变大时，显示反馈更重要。

实际上，对隐式信息进行整合，我们可以通过更直接的方式来获取更准确的结果，公式如下：

$\hat{r}_{ui} = b_{ui}+q^T_i(p_u+|N(u)|^{-\frac{1}{2}}\sum_{j \in N(u)}y_j) \quad \quad (15)$

以上面相比，在用户表示上添加$p_u$，其中$p_u$从用户显示评分数据中得到。使用$p_u+|N(u)|^{-\frac{1}{2}}\sum_{j \in N(u)}y_j$既有显示表示，又有隐式表示，我们称这种模型为SVD++

SVD++虽然没有参数更少，解释性更强的优点，但在Netflix数据上效果更好。

5. 整合模型

将邻居模型和SVD++融合

一种融合方式是将公式10和公式15的预测结果相加

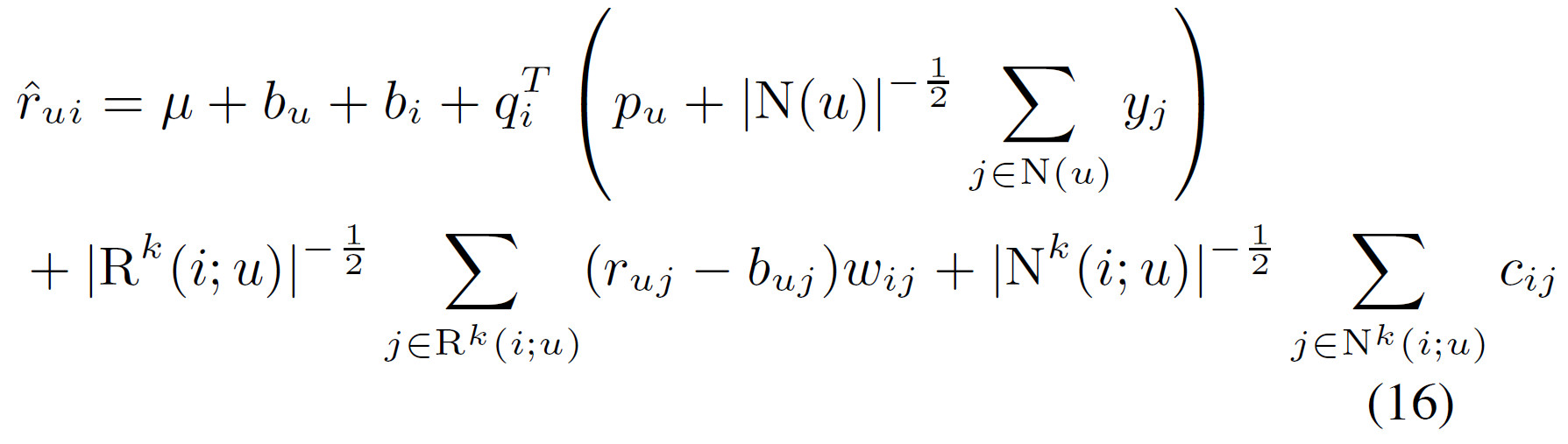
公式(16)提供了3层模型。

第一层$\mu+b_i + b_u$描述了商品和用户的一般属性，不考虑任何的交互。例如电影《指环王》拍的很好，用户Joe对所有电影的评分都是平均水平。
第二层$q^T_i(p_u+|N(u)|^{-\frac{1}{2}}\sum_{j \in N(u)}y_j)$提供了用户和物品的交互。例如用户Joe对《指环王》的科幻电影里评分较高
第三层邻域层贡，对其进行细粒度的调整，这种调整很难描述，例如用户Joe在“励志”标签的电影中评分较低。

模型参数通过梯度下降来更新。

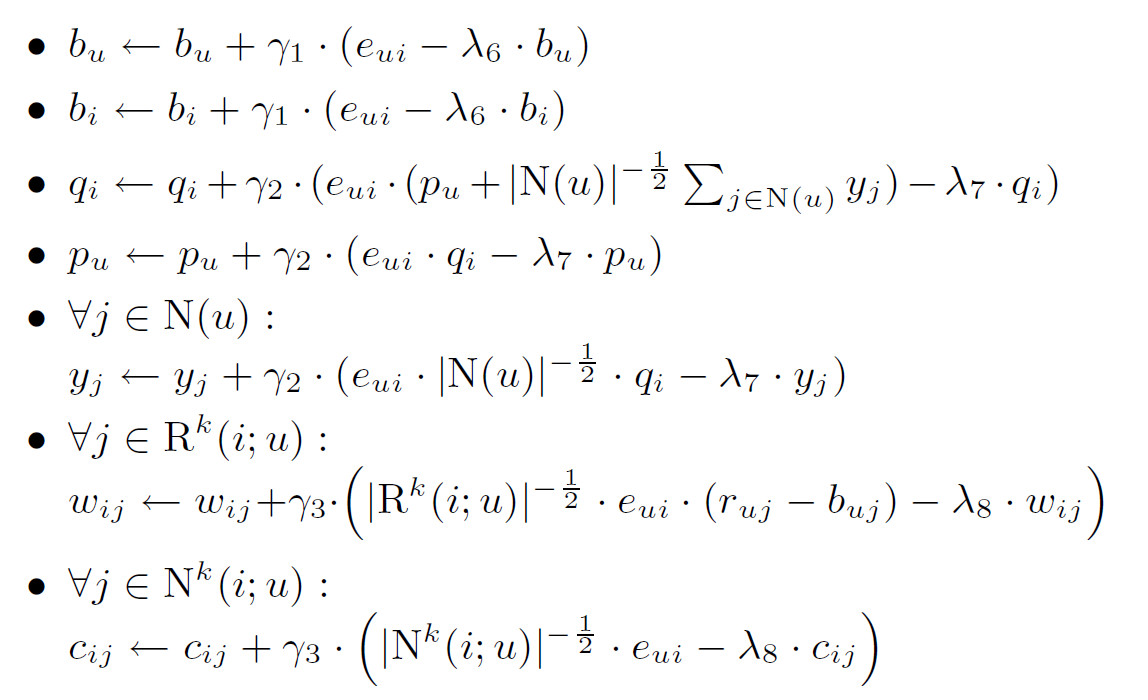
6. 总结

我们提出了新的邻居模型，该模型通过全局损失函数进行优化，具有可解释性强，并且可应对新用户，不用重新训练的问题。同时对SVD方法进行扩展，通过整合隐式反馈来提升准确率。

推荐系统的性能从不同的维度体现，例如准确率，多样性，推荐意想不到的物品的能力，可解释性，topK推荐，计算效率等。

远方到底有多远

SVD++介绍Factorization meets the neighborhood: a multifaceted collaborative filtering model