矩阵分解MF论文Matrix Factorization Techniques for Recommender Systems

这个论文是推荐算法中的经典论文，介绍的是矩阵分解FM，雅虎团队提出来的，发表在IEEE2009的computer期刊上，算法有效但非常简单。

作者Yehuda Koren是Netflix Prize的冠军队成员，是推荐系统领域的大神级人物。他带领的团队在 Netflix Prize 比赛中拿到过两次进步奖（progress award），参与的团队拿到过 2009 年 Netflix Prize 比赛的百万美金大奖。当年比赛的题目是 netflix 电影评分预测，Yehuda Koren 所在团队提出的算法在测试集上的均方根误差为 0.8567，比比赛开始时的最高成绩提高了 10.06%。Yehuda Koren在这篇论文中提出基于矩阵分解的算法，优于传统的最近邻基础，已经成为现在几乎所有推荐系统的基础。

论文地址

• 1. 推荐系统策略
• 2. 矩阵分解
  • 2.1. 随机梯度下降
  • 2.2. 交替最小二乘法ALS
  • 2.3. 添加偏差
  • 2.4. 丰富用户表示
  • 2.5. 时间动态性
  • 2.6. 带权正则矩阵分解
• 3. 矩阵分解的优点

电子零售商给消费者提供了大量的商品供用户选择，造成信息过载，向用户推荐匹配的商品可以提升用户的满意度和忠诚度，零售商通过分析用户在商品的兴趣模式，提供个性化推荐。

1. 推荐系统策略

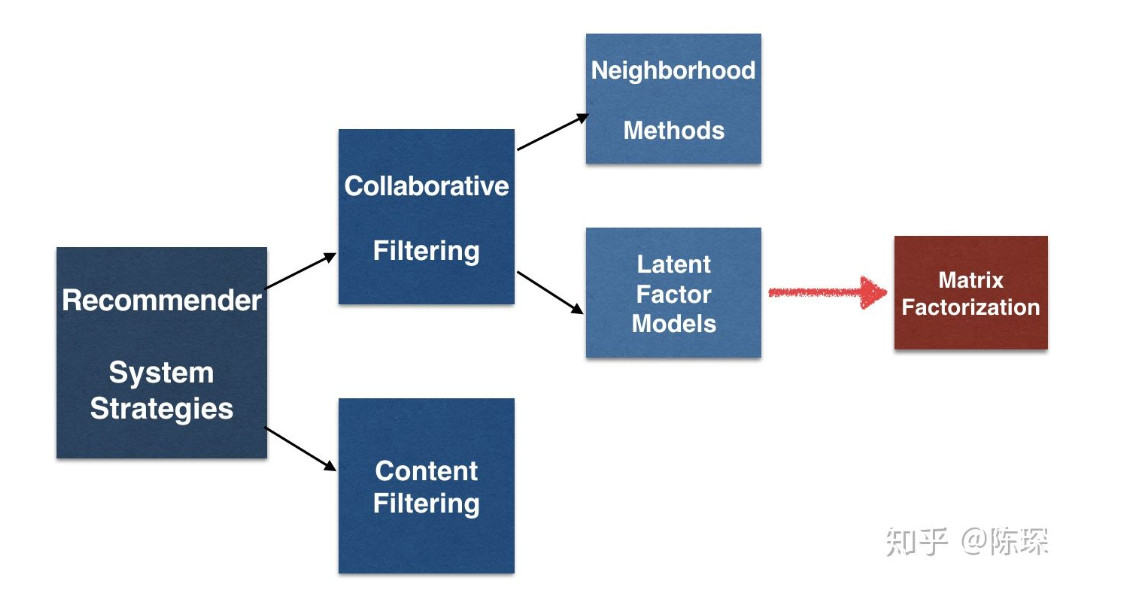
广义上讲，推荐系统基于2个策略：

1. 基于内容的策略
内容过滤策略给每个用户和商品创建一个画像表示其属性。例如电影画像包括主题，主演，票房等。用户画像包括人口统计信息或问卷调查信息。这些画像允许程序将用户和商品进行匹配。

2. 协同过滤
协同过滤又分为邻居模型和潜在因子模型。邻居模型有user-based和item-based，潜在因子模型有矩阵分解，例如SVD，SVD++等。
一种替代方法是基于用户的协同过滤，先找出用户-商品的评分矩阵，然后计算2个用户对商品的评分向量的相似性，而不是基于用户画像计算相似性。
但是基于用户的协同过滤需要用户对商品的评分计算相似性，因此会遇到冷启动的问题。在这方面，基于内容的推荐更胜一筹。

潜在因子模型根据评分模式推断出20~100个因子来表示商品或用户

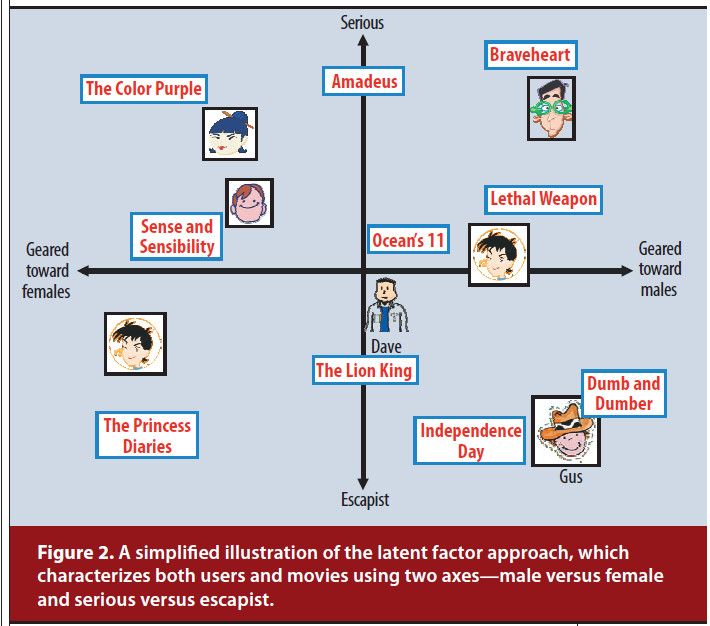
2. 矩阵分解

Matrix Factorization矩阵分解通过对用户-物品评分矩阵进行分解，使用因子向量表示用户和物品。

矩阵分解使用的是用户-物品的评分矩阵，但这个矩阵是很稀疏的，因为一个用户可能只评价了一小部分物品。

矩阵分解MF的一个优点是可以使用额外的信息。有时候显示的评分没法获取到，但我们可以使用一些隐式的信息来表示用户的兴趣，例如用户的浏览，购买记录，鼠标停留时间等。

通过矩阵分解，分别使用向量表示用户和物品。对于商品使用向量表示，向量中每个元素表示该商品和这个因素的相关程度。对于用户使用向量表示，向量中每个元素表示用户对这个因素的感兴趣程度，计算用户$u$对商品$i$的感兴趣程度，使用2个向量的内积表示

$$\hat{r}_{ui}=q^T_ip_u$$ $$q_i,p_u \in \mathbb{R}^f$$

矩阵分解的关键是怎么获取到用户向量$p_u$和物品向量$q_i$

矩阵分解模型有2种实现方法

1. 应用SVD对user-item评分矩阵进行分解，但有时user-item评分矩阵是很稀疏的。早期的系统会采用插值的方法使评分矩阵变得稠密，但这会增加工作量，另外不正确的插值会引入噪声。
2. 最近的方法一般直接对评分矩阵进行建模，同时使用正则化避免过拟合，使用梯度下降进行优化

$$J(p_u,q_i)= \frac{1}{2}(\sum_{r_{ui} \neq0}(r_{ui}-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2))$$

优化的目标是$min J(p_u,q_i)$，即让$\hat{r}_{ui}=q^T_ip_u$和$r_{ui}$尽可能接近

其中$r_{ui}$是已知的

最小化上述公式有2种方法：随机梯度下降和交替最小二乘法ALS

2.1. 随机梯度下降

$J(p_u,q_i)$对$p_u$求导得：

$$\frac{\delta J(p_u,q_i)}{p_u}=(r_{ui}-q^T_ip_u)(-q^T_i)+\lambda p_u$$

这里令$e_{ui}=r_{ui}-q^T_ip_u$

所以

$$\frac{\delta J(p_u,q_i)}{p_u}=-e_{ui}q^T_i+\lambda p_u$$

对$p_u$进行更新：

$$p_u=p_u-\eta \cdot \frac{\delta J(p_u,q_i)}{p_u} = p_u + \eta \cdot (e_{ui} \cdot q_i - \lambda \cdot p_u)$$

同理

$$q_i=q_i-\eta \cdot \frac{\delta J(p_u,q_i)}{q_i} = q_i + \eta \cdot (e_{ui} \cdot p_u - \lambda \cdot q_i)$$

2.2. 交替最小二乘法ALS

矩阵分解中最常用的是ALS进行优化

因为$p_u,q_i$两个变量未知，因此损失函数不是凸函数，无法使用凸优化求解。
但是，如果固定$p_u$，那么损失函数就只是关于$q_i$的二次函数，直接解二次函数即可。

因此，可固定$p_u$，求解$q_i$；再固定$q_i$，求解$p_u$，这样迭代下去。

• 固定$q_i$，求解$p_u$

  $$\frac{\delta J(p_u)}{p_u}=(r_{ui}-q^T_ip_u)(-q^T_i)+\lambda p_u=(q^T_iq_i+\lambda)p_u-r_{ui}q^T_i$$

  令$\frac{\delta J(p_u)}{p_u}=0$，写成矩阵的形式：

  $$(QQ^T+\lambda E)P = R_jQ^T$$

  $E$是全1矩阵
  求解得到：

  $$P = (QQ^T+\lambda E)^{-1}R_j$$

• 固定$p_u$，求解$q_i$

  同理求得：

  $$Q = (PP^T+\lambda E)^{-1}R_i$$

通常随机梯度下降比ALS更快，但是在以下2种情况下，ALS更有利：

1. 并行化，在ALS中，系统独立于其他项目因素计算每个$q_i$和$p_u$
2. 在以隐式数据为中心的系统中，训练集不是稀疏的，如果使用SGD，遍历每个训练样本是不切实际的，ALS可以处理这种情况

2.3. 添加偏差

在计算用户$u$对物品$i$的评分时，可以添加偏差。

$$b_{ui}=\mu + b_i + b_u$$

其中$\mu$是所有电影的平均评分，$b_i$是物品$i$的偏差，$b_u$是用户$u$的偏差。最终的预测评分为：

$$\hat{r}_{ui}=\mu + b_i + b_u + q^T_ip_u$$

假设现在你要预测Joe对《泰坦尼克号》的评分，令所有电影的评分$\mu=3.7$，而由于《泰坦尼克号》比一般电影好，评分高出$b_i=0.5$，而Joe对电影是一个挑剔的人，评分通常比平均低$b_u=0.3$分，则总的偏差为$3.7+0.5—.3=3.9$分

加上偏差，最终的损失函数为：

$$J(p_u,q_i,b^*)= \frac{1}{2}(\sum_{r_{ui} \neq0}(r_{ui}-\mu-b_u-b_i-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2+b^2_u+b^2_i))$$

2.4. 丰富用户表示

推荐系统需要解决冷启动问题，有些用户只有很少的评分，这样我们可以获取用户其他的隐式数据，例如浏览，购买记录等。

我们使用$N(u)$表示用户$u$显示了隐式喜好的物品集合，对于$N(u)$中的每个物品$i$使用$x_i \in \mathbb{R}^f$表示物品的特征，然后归一化：

$$|N(u)|^{-0.5} \sum_{i \in N(u)}x_i$$

除了以上特征，还有用户$u$的个人属性特征$A(u)$，例如年龄，收入等，对于每一个特征$y_a \in \mathbb{R}^f$,总的表示为：

$$\sum_{a \in A(u)}y_a$$

矩阵分解得到的预测得分变成下面式子：

$$\hat{r}_{ui}=\mu + b_i + b_u + q^T_i (p_u+|N(u)|^{-0.5} \sum_{i \in N(u)}x_i+\sum_{a \in A(u)}y_a)$$

上面增强了用户表示，同样也可以丰富物品的表示。

2.5. 时间动态性

现在为止，提出的模型都是静态的，实际上，用户的兴趣会随着时间变化。因此在考虑用户-物品的交互中需要考虑到时间动态性。

为了体现时间动态性，偏差都变成时间的函数，即物品偏差$b_i(t)$，用户偏差$b_u(t)$，用户偏好$p_u(t)$，不像人的喜好随时间变化，物品的特征一般是静态的，因此$q_i$不随着时间变化，现在用户$u$对物品$i$的评分变成：

$$\hat{r}_{ui}(t)=\mu + b_i(t)+b_u(t)+q^T_ip_u(t)$$

2.6. 带权正则矩阵分解

并不是现在所有的评分都赋予相同的权重，例如大量的广告可能会影响对某个商品的打分，后者系统中有些商品被恶意打分或刷好评等。

在有些场景下，虽然没有得到用户具体的评分，但是能够得到一些类似于“置信度”的信息（也称为隐式反馈信息），例如用户的游戏时长、观看时长等数据。虽然时长信息不能直接体现用户的喜好，但是能够说明用户喜欢的概率更大。

“带权”就是根据置信度计算每条记录对应损失的权重，优化的目标函数如下：

当没有得到用户具体的评分，但是能够得到一些类似于隐式反馈信息时，就可使用带权正则矩阵分解

$$J(p_u,q_i,b^*)= \frac{1}{2}(c_{ui}\sum_{r_{ui} \neq0}(r_{ui}-\mu-b_u-b_i-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2+b^2_u+b^2_i))$$

3. 矩阵分解的优点

1. 泛化能力强，在一定程度上解决数据稀疏问题
2. 空间复杂度低。不需要存储用户相似或物品相似矩阵，只需要存储用户和物品的隐向量。空间复杂度从$o(n^2)$降低到$o((n+m) \times k)$级别
3. 更好的扩展性和灵活性。矩阵分解最后得到用户和物品隐向量，这其实和深度学习的嵌入类似，因此矩阵分解与其他特征进行组合和拼接很方便

但矩阵分解也有一些局限。总的来说应该是整个协同过滤模型的局限，无法加入用户，物品属性，上下文信息，这丢失了很多有效信息。