Tucker分解

最近读论文，发现在交通领域中可以使用Tucker进行数据补全和降维，于是在网上查了下，下面是对于该技术简单记录。

多维的矩阵叫做张量，张量中有多维，有称为模(mode)

假设一个矩阵$R$一共有$N$维，$R \in \mathbb{R}^{I_1 \times I_2 …\times I_N}$

• 张量$n$-mode(沿第n模)展开是将N维张量$R$沿mode-n展开成一个二维矩阵$R_{(n)}$，其中$R_{(n)} \in \mathbb{R}^{I_n \times (I_1I_2…I_{n-1}I_{n+1}…I_{N})}$。假设三维张量$A \in \mathbb{R}^{I \times J \times K}$，展开后矩阵$A_{(1)} \in \mathbb{R}^{I \times (JK)}$，$A_{(2)} \in \mathbb{R}^{J \times (IK)}$，$A_{(3)} \in \mathbb{R}^{K \times (IJ)}$
• 张量与矩阵n-mode乘积。张量$R \in \mathbb{R}^{I_1 \times I_2 …\times I_N}$和矩阵$A \in \mathbb{R}^{J \times I_n}$的乘积$R \times A \in \mathbb{R}^{I_1 \times …\times I_{n-1} \times J \times I_{(n+1)} \times … \times I_N}$

$$\left(R \times_{n} A\right)_{i_{1} \cdots i_{n-1} j i_{n+1} \cdots i_{N}}=\sum_{i_{n}=1}^{I_{n}} r_{i_{1} i_{2} \cdots i_{n}} a_{j i_{n}}$$

张量分解是矩阵分解在高维数据中的扩展，典型的张量分解方法有CP分解和Tucker分解。下面只介绍Tucker分解。

Tucker分解将N维张量分解成一个核心张量G和N个因子矩阵沿各个mode的乘积

$$\begin{aligned} \mathcal{R} \approx & G \times_{1} \boldsymbol{A}^{(1)} \times_{2} \boldsymbol{A}^{(2)} \times \cdots \times_{N} \boldsymbol{A}^{(N)}=\\ & \sum_{i_{1}=1}^{J_{1}} \sum_{i_{2}=1}^{J_{2}} \ldots \sum_{i_{N}=1}^{J_{N}} G_{i_{i} i_{2} \cdots i_{N}} a_{i_{1}}^{(1)} \circ a_{i_{2}}^{(2)} \circ \cdots \circ a_{i_{N}}^{(N)} \end{aligned}$$

其中$\mathcal{R} \in \mathbb{R}^{I_1 \times I_2 …\times I_N}$是原始张量；核心张量$G \in \mathbb{R}^{J_1 \times J_2 …\times J_N}$；因子矩阵$\boldsymbol{A}^{(1)} \in \mathbb{R}^{I_1 \times J_1}$，$\boldsymbol{A}^{(2)} \in \mathbb{R}^{I_2 \times J_2}$，$\boldsymbol{A}^{(N)} \in \mathbb{R}^{I_N \times J_N}$。因子矩阵可以看做原始张量在每个mode上的主成分。

下面以3维张量做Tcuker分解为例：

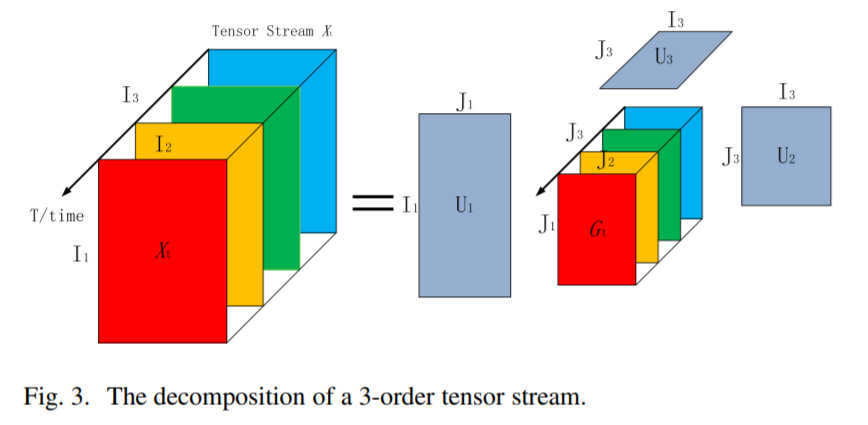
【参考资料】

面向交通数据的张量计算技术

浅析张量分解（Tensor Decomposition）

Travel Time Estimation of a Path using Sparse Trajectories

基于位置聚类和张量分解的Web服务推荐研究与应用