GMAN: A Graph Multi-Attention Network for Traffic Prediction

厦门大学在2020AAAI发表的一篇文章

1. 介绍

交通预测一般用来预测流量或速度。现在交通状态长期预测仍然存在以下挑战：

复杂的时空相关性
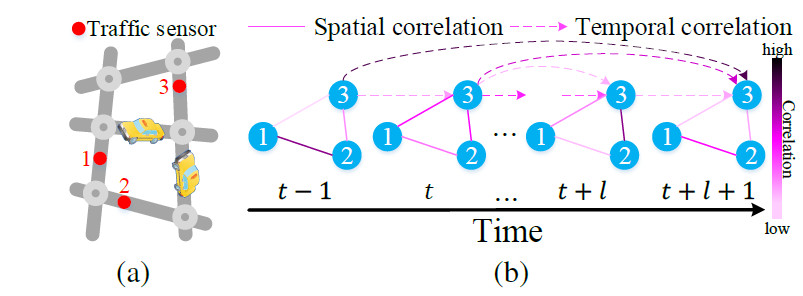
对错误传播敏感。

为了解决以上2个挑战，提出了GMAN，

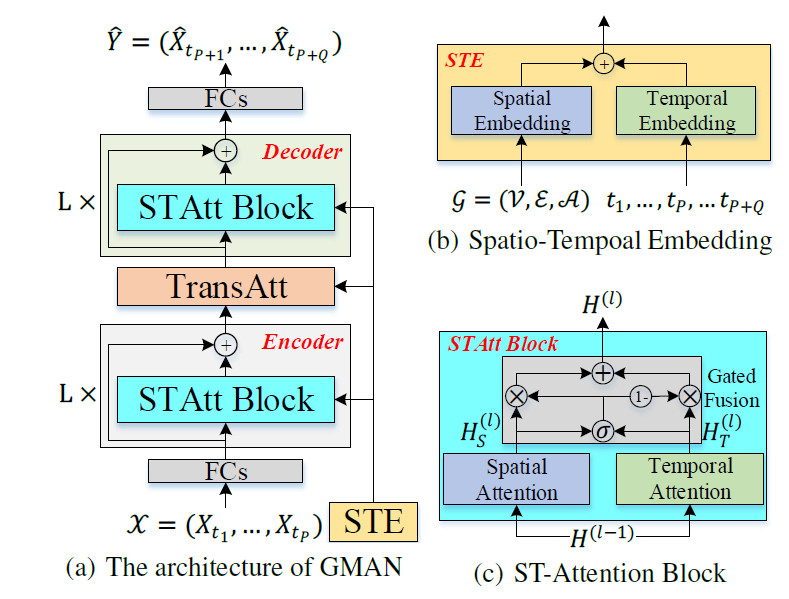
GMAN是一个encoder-decoder架构，
其中encoder和decoder中包含多个时空attention块。ST-Att块包括空间Att和时间Att。然后门控fusion对空间Att和时间Att的输出进行融合。
在encoder和decoder中间有一个transform attention层，用来转换encoder的输出结果，来作为decoder的输入。

2. 问题定义

$G=(V,E,A)，|V|=N，A \in \mathbb{R}^{N \times N}$,$A$中元素表示2个节点的距离。图信号矩阵$X_t \in \mathbb{R}^{N \times C}$。
给定历史$P$个时间段，预测未来$Q$个时间段

$\mathcal{X}=\left(X_{t_{1}}, X_{t_{2}}, \ldots, X_{t_{P}}\right) \in \mathbb{R}^{P \times N \times C}$ $\hat{Y} = \left(\hat{X}_{t_{P+1}}, \hat{X}_{t_{P+2}}, \ldots, \hat{X}_{t_{P+Q}}\right) \in \mathbb{R}^{Q \times N \times C}$

3. GMAN

Encoder和Deocder都包含L个ST-Att block。
每个STAtt block包含空间att和时间att，通过门控进行融合。
在encoder和decoder之间有一个Transform att层

3.1. Spatial-Temporal Embedding

包括空间embedding和时间embedding。

空间embedding：使用node2vec来学习图中节点的嵌入，并且嵌入矩阵中保留图的结构信息，即相邻的2个节点学到的节点嵌入相似。节点$i$的空间嵌入为$e^S_{v_i} \in \mathbb{R}^D$
时间embedding：将每一个时间步编码成一个向量。一天有T个时间段，将每个时间段使用dayOfWeek(7维)和timeOfDay(T维)来表示，然后拼接成$\mathbb{R}^{(7+T)}$，然后使用2个FCN进行嵌入成$\mathbb{R}^{D}$，使用$e^T_{t_j} \in \mathbb{R}^D$表示

然后将空间嵌入和时间嵌入融合，如图b所示。对于节点$v_i$在时间$t_j$，节点嵌入表示成$e_{v_i,t_j}=e^S_{v_i}+e^T_{t_j}$，则N个节点在$P+Q$个时间段的节点嵌入为$E \in \mathbb{R}^{(P+Q) \times N \times D}$

3.2. ST-Att Block

时空注意力块如图c所示。包括空间att+时间att+门控融合。

第$l$个时空注意力块的输入是$H^{(l-1)}$,输出为$H^{(l)}$
节点$v_i$在第$t_j$时间段的表示为$h^{(l-1)}_{v_i,t_j}$
在第$l$个块中空间att的输出表示为$H_S^{(l)}$，一个节点表示为$h_{S_{v_i,t_j}}^{(l)}$
在第$l$个块中时间att的输出表示为$H_T^{(l)}$,一个节点表示为$h_{T_{v_i,t_j}}^{(l)}$
提前定义非线性FC为：
$f(x)=\operatorname{ReLU}(x \mathbf{W}+\mathbf{b})$

3.2.1. Spatial-Att

节点之间会相互影响，且随着时间变化。空间att对不同的节点分配不同的权重。

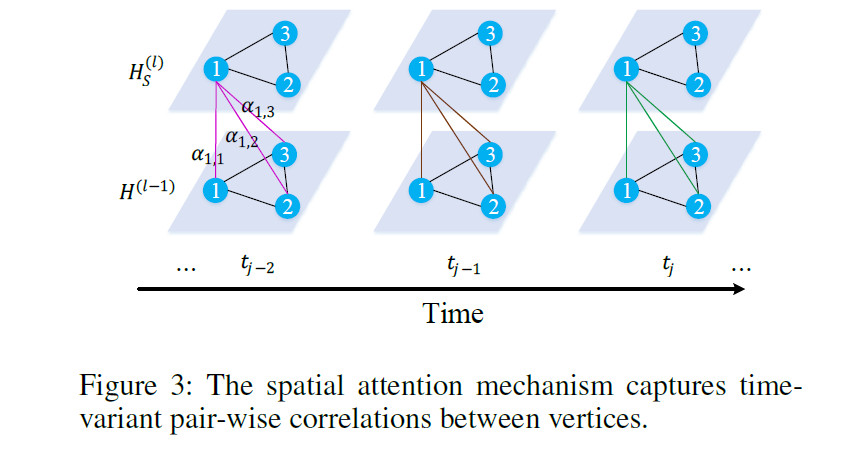
$h s_{v_{i}, t_{j}}^{(l)}=\sum_{v \in \mathcal{V}} \alpha_{v_{i}, v} \cdot h_{v, t_{j}}^{(l-1)}$

$\mathcal{V}$表示所有的节点，$\alpha_{v_{i}, v}$表示节点$v$对节点$v_i$的重要性。

下面介绍$\alpha_{v_{i}, v}$怎么计算的。在某个时间段，当前的交通状况和路网结构都会影响节点间的相关性。例如一条道路拥堵可能会影响到邻居节点的交通状况。基于此，我们考虑交通特征和图结构来学习attention分数。将上一层时空att块的输出$h^{(l-1)}$和时空嵌入$e$拼接，然后使用缩放的点积相乘计算节点$v_i$和$v$的相关性。

$s_{v_{i}, v}=\frac{\left\langle h_{v_{i}, t_{j}}^{(l-1)}\left\|e_{v_{i}, t_{j}}, h_{v, t_{j}}^{(l-1)}\right\| e_{v, t_{j}}\right\rangle}{\sqrt{2 D}}$

然后再使用softmax归一化

$\alpha_{v_{i}, v}=\frac{\exp \left(s_{v_{i}, v}\right)}{\sum_{v_{r} \in \mathcal{V}} \exp \left(s_{v_{i}, v_{r}}\right)}$

为了稳定学习过程，我们将学习注意力机制扩展为多头注意力机制,然后再将$K$个头的结果拼接在一起。

$\begin{array}{c} s_{v_{i}, v}^{(k)}=\frac{\left\langle f_{s, 1}^{(k)}\left(h_{v_{i}, t_{j}}^{(l-1)} \| e_{v_{i}, t_{j}}\right), f_{s, 2}^{(k)}\left(h_{v, t_{j}}^{(l-1)} \| e_{v, t_{j}}\right)\right\rangle}{\sqrt{d}} \\\\ \alpha_{v_{i}, v}^{(k)}=\frac{\exp \left(s_{v_{i}, v}^{(k)}\right)}{\sum_{v_{r} \in \mathcal{V}} \exp \left(s_{v_{i}, v_{r}}^{(k)}\right)} \\\\ h_{s_{v_{i}, t_{j}}}^{(l)}=\|_{k=1}^{K}\left\{\sum_{v \in \mathcal{V}} \alpha_{v_{i}, v}^{(k)} \cdot f_{s, 3}^{(k)}\left(h_{v, t_{j}}^{(l-1)}\right)\right\} \end{array}$

$f^{(k)}_{s,1}(\cdot),f^{(k)}_{s,2}(\cdot),f^{(k)}_{s,3}(\cdot)$表示ReLU非线性变换。$d=\frac{D}{K}$

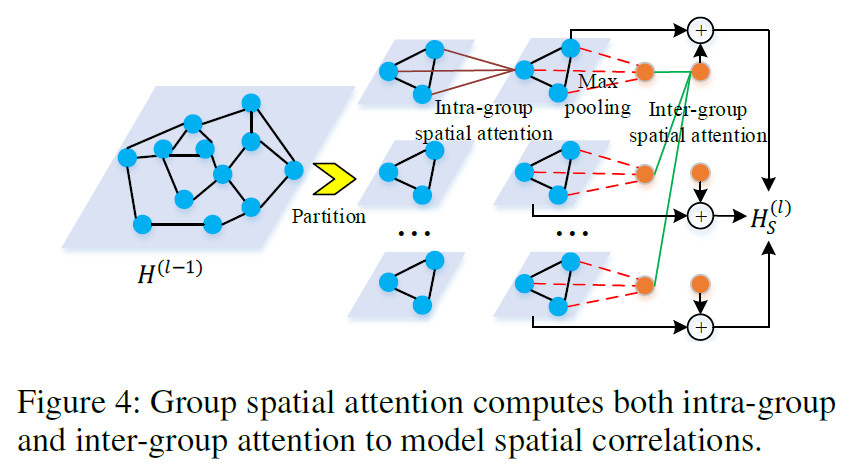
如果图中节点$N$非常大，计算attention时需要$N^2$的时间复杂度，为了解决这个问题，我们提出分组空间attention，包括组内空间attention和组间空间attention。

随机将$N$个节点分成$G$组，每个组内有$M=\frac{N}{G}$个节点。先使用上面的3个公式得到每个组组内（local）的attention，计算得到$h$。然后再进行最大池化，将多个节点变成一个节点的表示。然后再计算组间的空间attention，生成每个组的全局特征。将局部特征和全局特征相加得到最终的输出。

3.2.2. Temporal-Att

在一个区域的交通状况和它前面时间段的交通状态有关，并且这种相关性随着时间变化。通过时间attention来学习不同时间段的重要性。如图5所示，使用下面公式计算节点$v_i$中$t_j$和$t$的相关性：

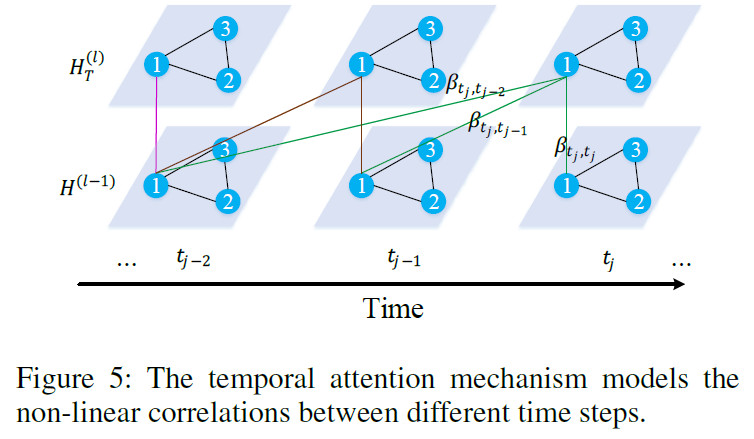
$\begin{array}{c} u_{t_{j}, t}^{(k)}=\frac{\left\langle f_{t, 1}^{(k)}\left(h_{v_{i}, t_{j}}^{(l-1)} \| e_{v_{i}, t_{j}}\right), f_{t, 2}^{(k)}\left(h_{v_{i}, t}^{(l-1)} \| e_{v_{i}, t}\right)\right\rangle}{\sqrt{d}} \\\\ \beta_{t_{j}, t}^{(k)}=\frac{\exp \left(u_{t_{j}, t}^{(k)}\right)}{\sum_{t_{r} \in \mathcal{N}_{t_{j}}} \exp \left(u_{t_{j}, t_{r}}^{(k)}\right)}\\\\ h_{t_{v_{i}, t_{j}}}^{(l)}=\|_{k=1}^{K}\left\{\sum_{t \in \mathcal{N}_{t_{j}}} \beta_{t_{j}, t}^{(k)} \cdot f_{t, 3}^{(k)}\left(h_{v_{i}, t}^{(l-1)}\right)\right\} \end{array}$

$\mathcal{N}_{t_{j}}$表示$t_j$之前的时间段。

3.2.3. 门控融合

使用门控机制来融合空间和时间表示。在第$l$个时空att块中，空间att的输出为$H_S^{(l)}$，时间att的输出为$H_T^{(l)}$，在encoder中这2个输出的维度都是$\mathbb{R}^{P \times N \times D}$，在decoder中这2个输出的维度都是$\mathbb{R}^{Q \times N \times D}$

$H^{(l)}=z \odot H_{S}^{(l)}+(1-z) \odot H_{T}^{(l)}$ $z=\sigma\left(H_{S}^{(l)} \mathbf{W}_{z, 1}+H_{T}^{(l)} \mathbf{W}_{z, 2}+\mathbf{b}_{z}\right)$

其中$\mathbf{W}_{z, 1} \in \mathbb{R}^{D \times D},\mathbf{W}_{z, 2} \in \mathbb{R}^{D \times D},\mathbf{b}_{z} \in \mathbb{R}^D$,$z$是门控。

3.3. Transform Attention

为了缓解预测时间步间的错误传播，我们在encoder和decoder之间添加了转换层，其建模了未来时间步和历史时间步的直接关系，对历史时间步的交通特征进行编码，生成未来的表示作为decoder的输入。

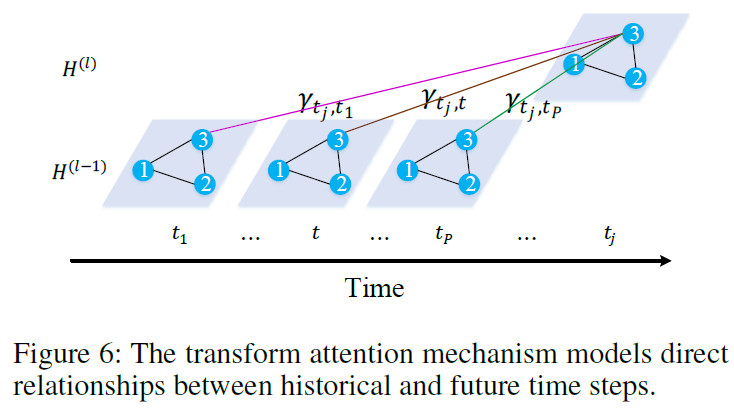
如图6所示，对于节点$v_i$，被预测时间步$t_j$和历史时间步$t (t=t_1,…t_P)$的相关性通过下面的式子计算

计算$t_j$和$t$的相关性 $\lambda_{t_{j}, t}^{(k)}=\frac{\left\langle f_{t r, 1}^{(k)}\left(e_{v_{i}, t_{j}}\right), f_{t r, 2}^{(k)}\left(e_{v_{i}, t}\right)\right\rangle}{\sqrt{d}}$
将$t_j$与$t_1$~$t_P$的相关性归一化
$\gamma_{t_{j}, t}^{(k)}=\frac{\exp \left(\lambda_{t_{j}, t}^{(k)}\right)}{\sum_{t_{r}=t_{1}}^{t_{P}} \exp \left(\lambda_{t_{j}, t_{r}}^{(k)}\right)}$
对$t_1$~$t_P$的输出进行融合，得到decoder的输入
$h_{v_{i}, t_{j}}^{(l)}=\|_{k=1}^{K}\left\{\sum_{t=t_{1}}^{t_{P}} \gamma_{t_{j}, t}^{(k)} \cdot f_{t r, 3}^{(k)}\left(h_{v_{i}, t}^{(l-1)}\right)\right\}$

Encoder-Decoder

GMAN是一个encoder-decoder架构，

输入数据是$X \in \mathbb{R}^{P \times N \times C}$，然后输入到FC中，生成$H^{(0)} \in \mathbb{R}^{P \times N \times D}$，同时STE生成时空嵌入$E \in \mathbb{R}^{(P+Q) \times N \times D}$。
$H^{(0)}$和$E$输入到L个时空注意力block中，输出$H^{(L)} \in \mathbb{R}^{P \times N \times D}$
然后转换层对$H^{(L)}$进行编码，生成未来序列表示$H^{(L+1)} \in \mathbb{R}^{Q \times N \times D}$
在decoder中堆叠L个时空注意力block，输出$H^{(2L+1)} \in \mathbb{R}^{Q \times N \times D}$
后跟一个FC，生成最终的结果$\hat{Y} \in \mathbb{R}^{Q \times N \times D}$

Loss

MAE损失函数

$\mathcal{L}(\Theta)=\frac{1}{Q} \sum_{t=t_{P+1}}^{t_{P+Q}}\left|Y_{t}-\hat{Y}_{t}\right|$