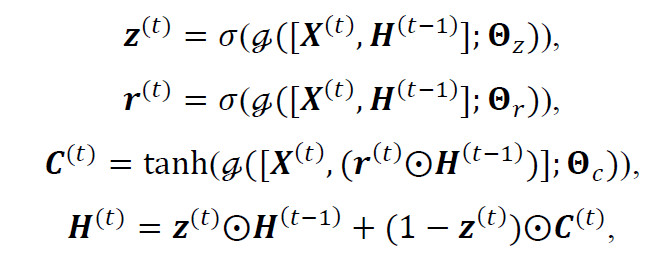Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting

发表于 | 分类于 | 浏览 次
字数统计: 2.1k | 阅读时长 ≈ 8

Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting

发表于AAAI2020

1. 介绍

本文的任务是给定一个道路图历史的交通数据，预测未来的交通状况。该任务主要有以下2个挑战：

  1. 不规则的路网导致交通数据间存在复杂时空依赖
  2. 各种各样不可预测的交通状况，使得交通数据具有不确定性

以前的工作一般使用CNN来处理网格数据，使用GCN+RNN(DCRNN)或GCN+CNN(STGCN)来处理图数据。但是这些方法仍然忽略了以下2方面：

  1. 原先的方法使用GCN都是基于一个固定的权重矩阵。如下图所示，图中有3个节点，其中节点1和3，节点2和3通过道路连接，现在的方法基本都是根据节点之间的距离来创建图，图的权重权重是不变的，但节点之间的权重并不是一成不变的，这种构图方法忽略了节点之间复杂的影响关系。

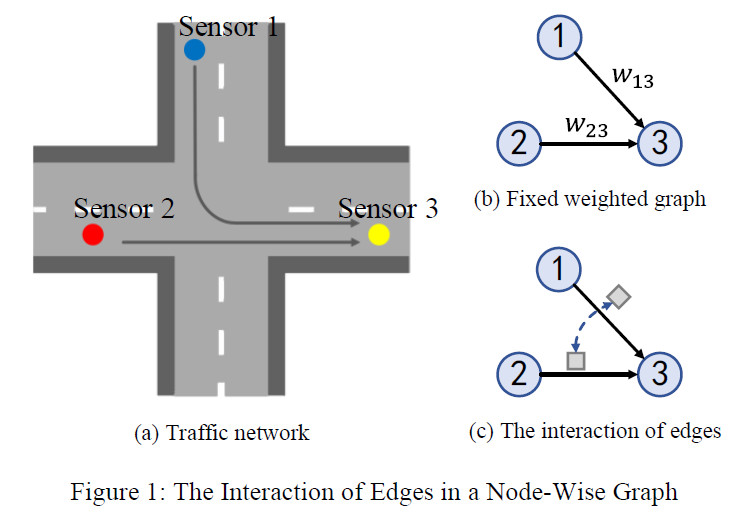
  1. 构建完图后，原先的方法一般使用GCN融合K跳邻居的信息进行聚合，但是却忽略了多个范围(multiple range)的信息。不同范围的信息反映了不同的交通属性。小范围的邻居揭示了局部依赖，大范围的邻居揭示了全局模式。并且不同范围的信息应该有不同的贡献。例如在一次交通事故中，目标区域主要受邻接区域的影响，所以模型也应该更关注这些区域，而不是对所有的K跳邻居都赋予相同的权重。

为了解决以上2个问题，我们提出Multi-Range Attentive Bicomponent Graph Convolutional Network (MRA-BGCN),不仅考虑了节点信息，而且把边作为实体，考虑边之间的交互。如图1(C)所示。该文章的共享如下：

  1. 提出MRA-BGCN，引入bicomponent图卷积，同时建模节点和边的相关性。节点图根据路网距离来构架，边图的构建考虑了2种模式：stream连通性、竞争关系。

  2. 为bicomponent图卷积提出多范围的attention机制，可以聚合不同范围的邻居信息并学到它们的权重

  3. 在METR-LA和PEMS-BAY这2个数据集上进行实验

2. 相关工作

DCRNN和STGCN使用固定的图结构
Graph WaveNet通过学习自适应的邻接矩阵来解决这个问题，但是隐藏的空间依赖是以数据驱动的方式来学习的，缺乏领域知识的指导，可能会出现过拟合的问题。

现有的方法无法对边之间的交互进行建模。

3. 问题定义

$G=(V,E,A),|V|=N$，其中$A \in \mathbb{R}^{N \times N}$表示邻接矩阵，邻接矩阵通过路网的距离构建。图信号矩阵$X^{(t)} \in \mathbb{R}^{N \times P}$。预测任务是给定历史$T’$个时间段的图信号矩阵，预测未来$T$个时间段的图信号矩阵

$X^{\left(t-T^{\prime}+1\right): t} \in \mathbb{R}^{N \times P \times T’}$，$X^{(t+1):(t+T)} \in \mathbb{R}^{N \times P \times T}$

本文中用到的图卷积定义如下：

4. MRA-BGCN

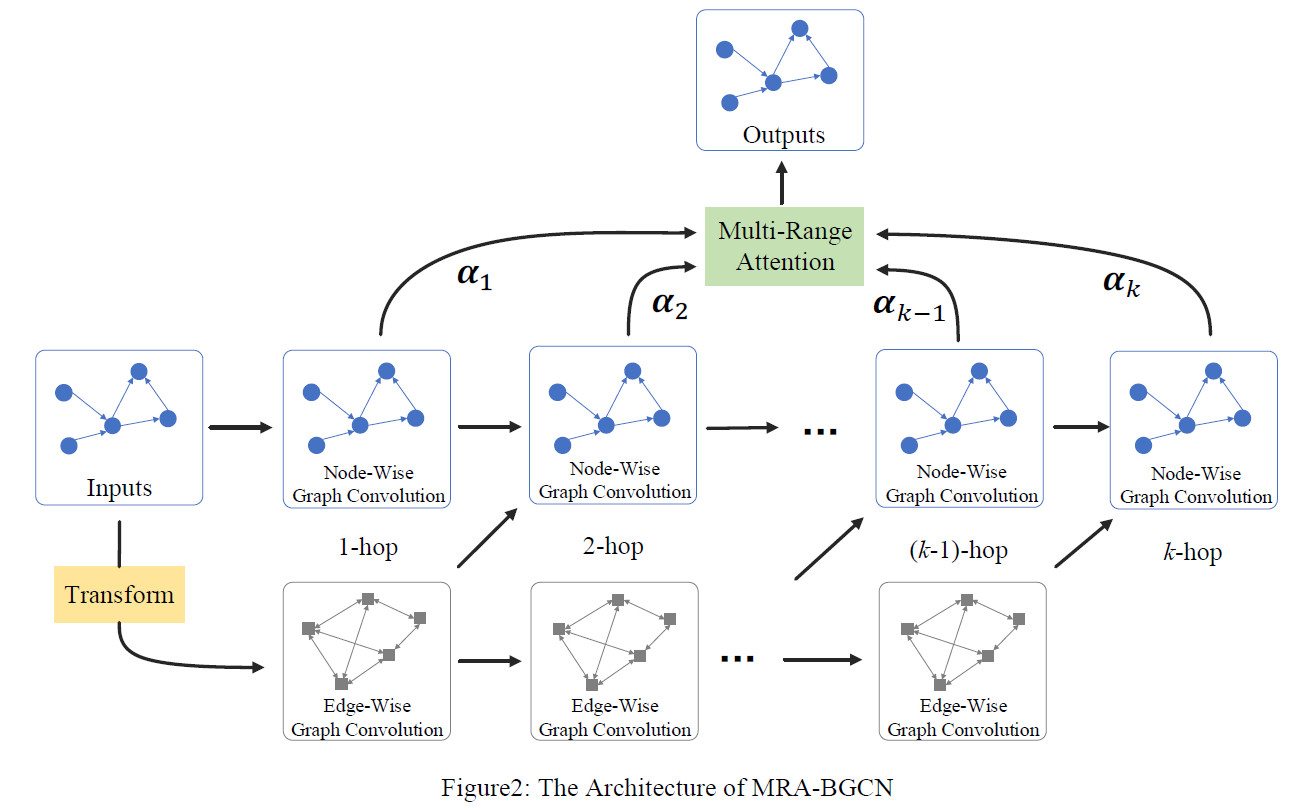
该模型包括2部分：bicomponent图卷积模块、多范围attention模块。

  • bicomponent图卷积模块包括节点图卷积、边图卷积，可以显式建模节点和边的相关性。
  • 多范围attention层聚合不同范围的邻居信息，并学习它们的重要性权重。
  • 除此之外，我们还将MRA-BGCN和RNN结合起来建模时间依赖。

4.1. Bicomponent GCN

首次创建2个图：节点图、边图

$G=(V,E,A)$表示节点图，$|V|=N$，每个节点表示sensor，边表示sensor之间的距离，邻接矩阵是权重邻接矩阵。

$G_e=(V_e,E_e,A_e)$表示边图,其中$|V_e|=|E|$，每个节点表示$E$中一条边。在邻接矩阵$A_e$中，有2种边的连接模式。

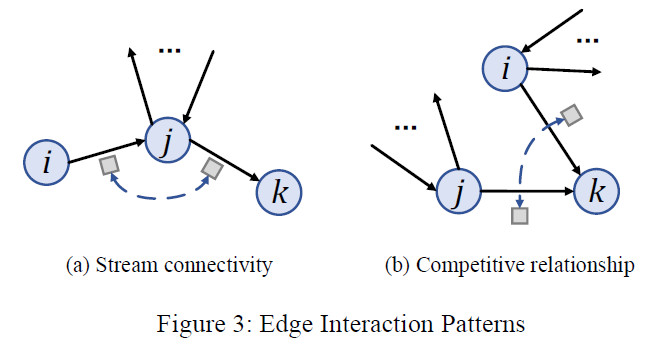
  • 上下游连接：如下图a所示，边(i,j)是边(j,k)的上游边，因此这2条边是相关的。如果点j有很多邻接，也就是说点j的度很大，则边(i,j)和边(j,k)的相关性就变得很弱。我们使用下面的公式计算这2条边的相关性。

    其中$\mathrm{deg}^{-}(j)$和$\mathrm{deg}^{+}(j)$表示点j的入度和出度。$\sigma$表示节点度的标准差。

  • 竞争连接：当2个节点共享一个源节点或目标节点，可能会争夺交通资源，使得这2条边产生竞争关系。如下图b所示。边(j,k)和边(i,k)共享目标节点k，如果源节点有很多邻居，则(j,k)和(i,k)的竞争连接就会变强。使用下面的公式计算这2条边的连接权重：

根据上面2种连接，构建好边图$G_e$，如图2所示，bicomponent图卷积可以建模节点和边的相关性。

下面做bicomponent GCN的步骤是：

现在有节点图和边图，已知节点图的图信号矩阵$X$,但是不知道边图的图信号矩阵。

  1. 根据节点图的图信号矩阵$X \in \mathbb{R}^{N \times P}$,和$M \in \mathbb{R}^{|V| \times |E|}$相乘得到边图的图信号矩阵$Z \in \mathbb{R}^{|E| \times P}$，然后再和$W_b$相乘做一个线性变换，得到$Z \in \mathbb{R}^{|E| \times P}$
  2. 然后对节点图$X$做GCN操作，得到下一层的输出$X^{(l)} \in \mathbb{R}^{N \times P}$
  3. 对边图$Z$做GCN操作，得到下一层的输出$Z^{(l)} \in \mathbb{R}^{|E| \times D}$
  4. 然后将这2个图信号矩阵拼接，再做一次GCN操作，得到$X^{(l+1)}$
  • 每个节点图的图信号矩阵$X^{(l+1)}$都是由$X^{(l)}$和$Z^{(l)}$计算得到
  • 每个边图的图信号矩阵$Z^{(l+1)}$都是由自己的$Z^{(l)}$计算得到。

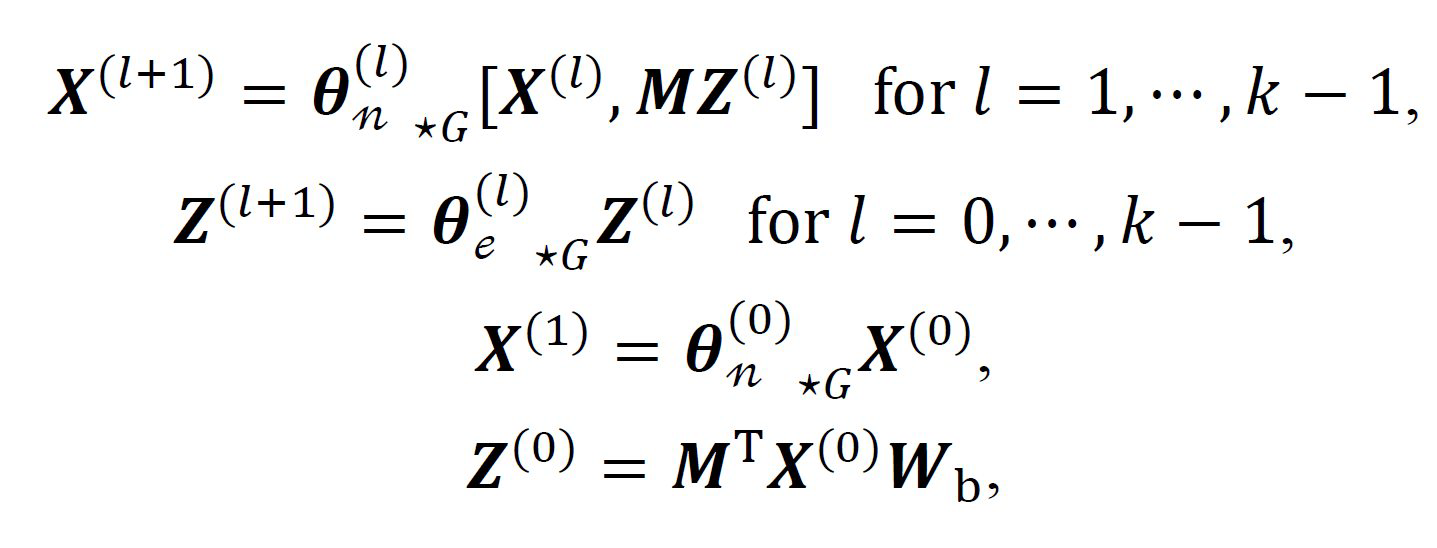
$X^{(l-1)}$是第$l$层节点图卷积层的输入，$Z^{(l-1)}$是第$l$层边图卷积的输入。$M \in \mathbb{R}^{|V| \times |E|}$表示节点和边的关联矩阵。$M_{i,(i,j)}=M_{j,(i,j)}=1$，通过$MZ^{(\cdot)}$聚合每个节点的边的表示。$M^TX^{(\cdot)}$聚合每条边的节点表示。$W_b$是可学习的矩阵，从原始的节点输入$X^{(0)}$转换成边输入$Z^{(0)}$

4.2. Multi-Range Attention

提出多范围attention机制来自动学习不同范围邻居的权重。

通过bicomponent图卷积，我们可以得到不同范围邻居的节点表示：$\boldsymbol{X}=\left\{\boldsymbol{X}^{(1)}, \boldsymbol{X}^{(2)}, \cdots, \boldsymbol{X}^{(k)}\right\}, \boldsymbol{X}^{(l)} \in \mathbb{R}^{|V| \times F}$。多范围attention层主要是就是不同范围的邻居信息，形成一个整合的节点表示。为了实现这个目标，首先一个共享的线性变换成$W_a \in \mathbb{R}^{F \times F’}$，作用在不同层的节点表示$X^{(l)}$上。

对于节点$i$，首先进行线性变换$W_aX^{(l)}_i$，$u$表示邻居上下文嵌入向量，是可学习参数。

通过多范围Attention机制，对不同跳的邻居赋予不同的权重，得到最终的图信号矩阵。

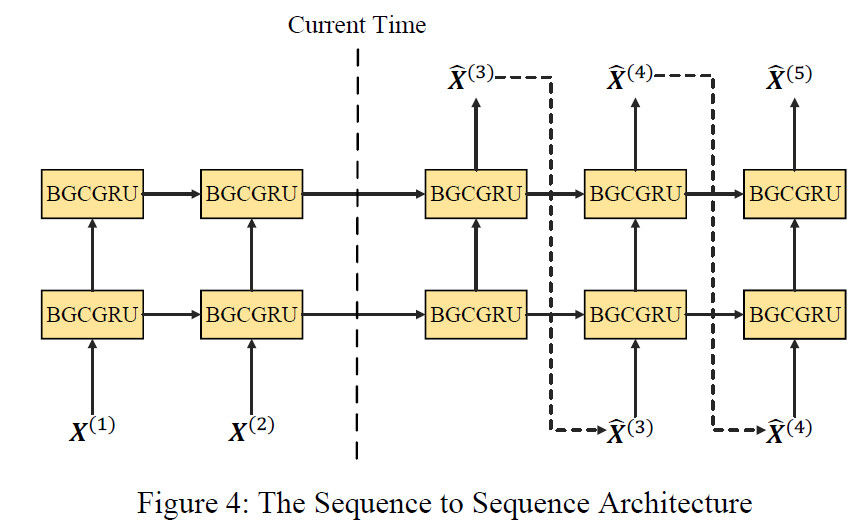
4.3. 结合RNN

参考DCRNN，把GRU中的全连接操作全都换成MRA-BGCN操作。

打赏
0%