2018ICLR的一篇论文:Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting
时空预测主要有以下挑战:
- 基于道路网络,存在复杂的空间依赖
- 交通状态会随着时间变化,存在动态性
- long-term预测比较困难
基于以上问题,本文根据交通流量的扩散过程,构建一个有向图,并且引入扩散卷积+RNN=DCRNN,融合时间和空间依赖,预测交通流量。DCRNN通过在图上进行双向随机游走来捕获空间依赖,使用encoder-decoder来捕获时间依赖。
1. 介绍
本文研究的主要任务是:在道路图上进行交通速度预测。
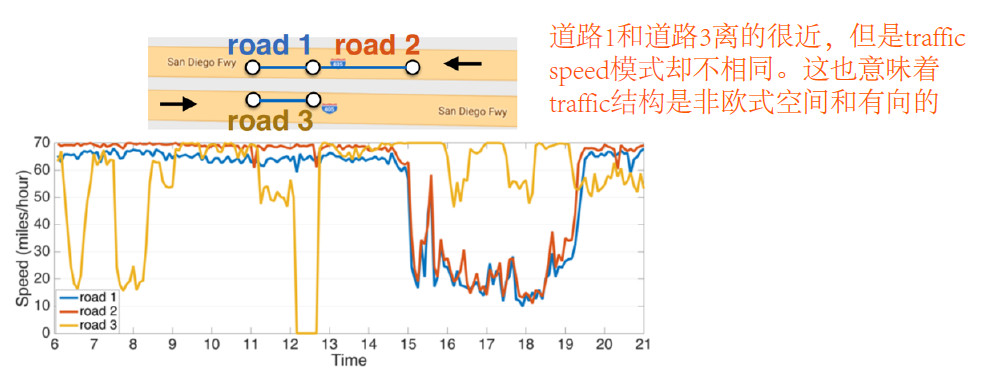
下图中给出了3条路的交通速度,道路1和道路3虽然离得很近,但是速度模式却完全不同,说明交通速度的空间结构是非欧式且有向的。
DCRNN = 扩散卷积 + encoder-decoder + 采样技术
2. 问题定义
首先构建一个有向图。
- 节点:sensor线圈感知器,$N$个节点
- 边的权重:2个sensor在道路上的距离,$W \in \mathbb{R}^{N \times N}$表示图的权重邻接矩阵
- 图信号矩阵$X \in \mathbb{R}^{N \times P}$,表示每个节点的traffic flow,speed
- 给定历史$T’$个时间段,预测未来$T$个时间段
3. DCRNN
3.1. 空间依赖建模
在图上进行随机游走,重启概率是$\alpha \in [0,1]$,状态转移矩阵$D^{-1}_OW$.其中$D_O=diag(W \mathbf{1})表示图的出度$, $\mathbf{1}$表示全1的向量。经过很多次的随机游走,这样的马尔科夫过程逐渐收敛到一个静态的分布$\mathcal{P} \in \mathbb{R}^{N \times N}$,其中第$i$行$\mathcal{P}_{i,:} \in \mathbb{R}^N$表示从节点$i$到其他节点的扩散可能性大小。
下面是在图上无限次随机游走的转移矩阵
其中$k$表示转移的次数,我们通常使用有限次的$K$步转移矩阵。
扩散卷积
下面给出扩散卷积的计算公式:
这是一个特征的扩散卷积操作。
其中$p$表示第$p$个特征,为每个特征计算一个扩散性。$\theta \in \mathbb{R}^{K \times 2}$是扩散卷积核参数,$\boldsymbol{D}_{O}^{-1} \boldsymbol{W}$和$\boldsymbol{D}_{I}^{-1} \boldsymbol{W}^{\top}$表示扩散过程中的转移矩阵和逆转移矩阵。
扩散卷积层
基于上面的扩散卷积操作,定义扩散卷积层,将每个节点$P$维特征映射成$Q$维特征。
其中$\boldsymbol{\Theta} \in \mathbb{R}^{Q \times P \times K \times 2}$, $\boldsymbol{\Theta}_{q, p,:,:} \in \mathbb{R}^{K \times 2}$
$\boldsymbol{X} \in \mathbb{R}^{N \times P}$表示输入图信号矩阵,$\boldsymbol{H} \in \mathbb{R}^{N \times Q}$表示输出图信号矩阵。在扩散卷积层,假设每个节点有3个特征,则就有3个扩散表示,然后再把这3个扩散表示加起来。
和谱图卷积的关系
扩散卷积可以定义在有向图上或无向图上。当应用在无向图上,现在的谱图卷积,例如ChebNet就可以看做是扩散卷积的特例。
3.2. 时间动态性建模
利用GRU来建模时间依赖。将GRU中矩阵相乘,全都变成扩散卷积操作。
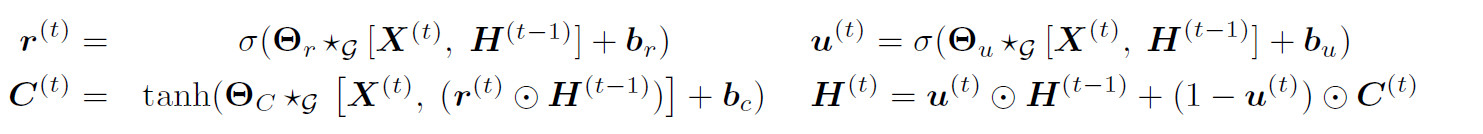
3.3. Encoder-Deocder
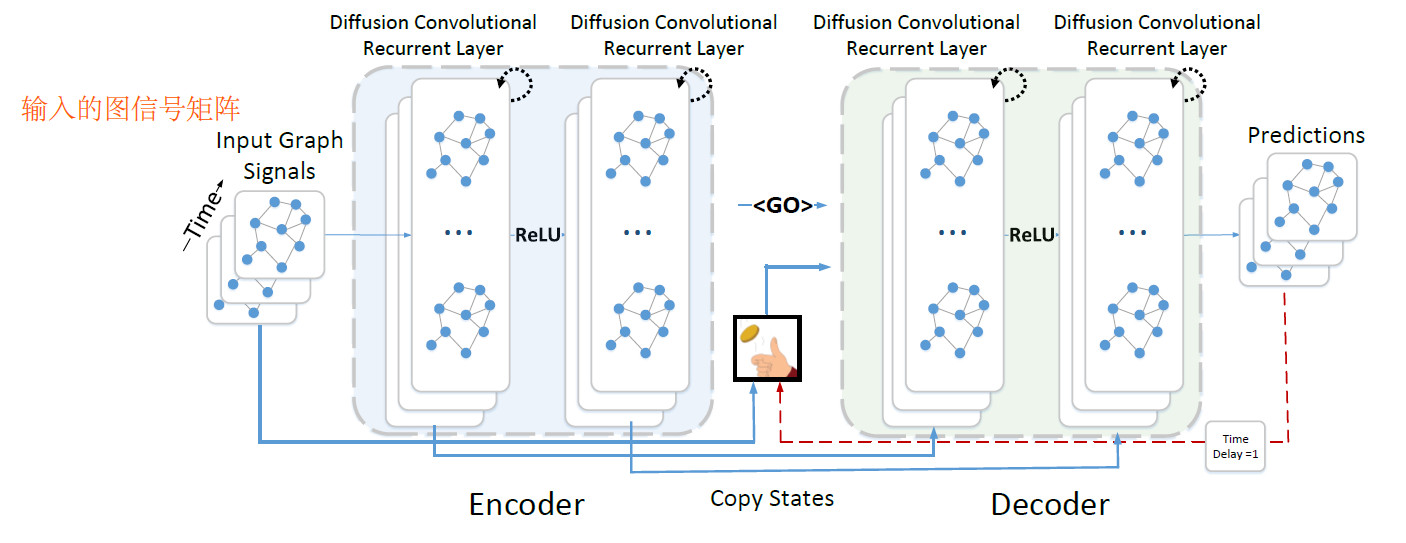
因为本文在时间上是多对多的预测,这里使用seq2seq架构。其中encoder和decoder都是DCGRU模型。
在训练阶段,将历史时间序列输入到encoder中,然后使用最后一个时间段的隐藏状态初始化decoder。
【注意】
- 在训练阶段,decoder使用上一个时间段的真值作为输入,进行预测
- 在测试阶段,由于获取不到真值,使用上一个时间段模型的预测值作为输入。
但是上面这种训练方法会导致训练和测试的输入分布不同,导致预测性能下降,为了解决这个问题,本文在训练阶段,不全部使用真值作为decoder的输入,而是以概率$\epsilon_i$输入真值,以$1-\epsilon_i$输入上个时间段的预测值。这样可以保证训练和预测中,decoder的输入分布不会差别太多。
4. 实验
4.1. 数据集
2个数据集
- METR-LA:洛杉矶高速公路的车辆速度,207个节点
- PEMS-BAY:加州,325个节点
下图是这2个数据集中节点的分布情况。
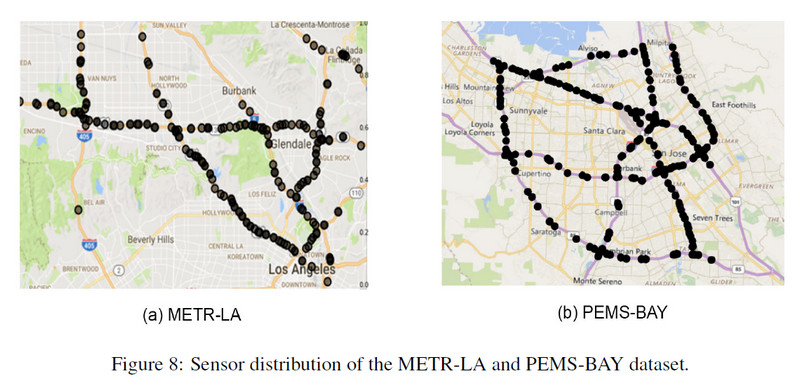
这2个数据集,都是5min聚合一次,使用Z-score归一化。训练集:验证集:测试集=7:1:2。
根据任意2个节点的距离构建邻接矩阵,如果$\operatorname{dist}\left(v_{i}, v_{j}\right) <= k$,则邻接矩阵中为0,否则为$W_{i j}$
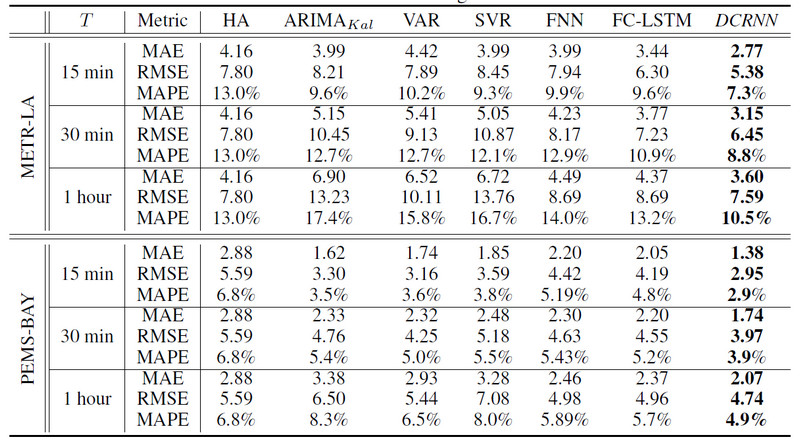
4.2. 实验结果