Graph WaveNet for Deep Spatial-Temporal Graph Modeling

论文地址：Graph WaveNet for Deep Spatial-Temporal Graph Modeling

• 1. 动机
• 2. 问题定义
• 3. 模型设计
  • 3.1. 图卷积层
  • 3.2. 时间卷积层

1. 动机

现在的时空图建模都是在一个静态图上进行建模，即图的邻接矩阵不变，并且现有的方法一般使用RNN或CNN来捕获时间特征，不能捕获长期的时间依赖。为了解决这2个限制，提出Graph WaveNet，图的邻接矩阵随时间变化，在时间维度上使用1D空洞卷积来捕获长期依赖。

为了捕获时空数据，现在一般有2种方法：

1. GCN+RNN
2. GCN+CNN

但是这2种方法中2个节点的相互依赖都建立在连接的基础上，但有些节点不连接仍然存在相互依赖的关系；当前的这种方法没有很有效的学习到时间依赖，RNN耗时且存在梯度消失问题，CNN可以并行，但需要堆叠很多层。

2. 问题定义

定义图$G=(V,E)$,其中邻接矩阵$A$非0即1，在第$t$个时间步，图信号矩阵$X^{(t)}\in \mathbb{R}^{N \times D}$

给定图$G$和历史$S$个时间段的图信号矩阵，预测未来$T$个时间段的图信号矩阵。

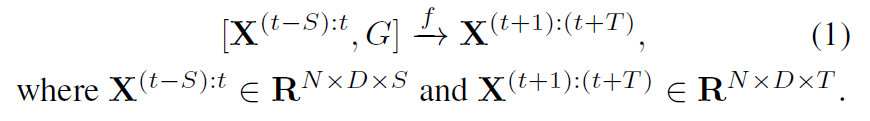
3. 模型设计

3.1. 图卷积层

在介绍之前，我们先看一下DCRNN提出的扩散矩阵操作：

1. 无向图

$$\mathbf{Z}=\sum_{k=0}^{K} \mathbf{P}^{k} \mathbf{X} \mathbf{W}_{\mathbf{k}}$$

其中$\mathbf{P}$是转移矩阵，如果是无向图的话，$\mathbf{P}=\mathbf{A} / \operatorname{rowsum}(\mathbf{A})$

2. 有向图

如果是有向图的话，需要计算入的方向和出的方向。
$\mathbf{P}_{f}=\mathbf{A} / \operatorname{rowsum}(\mathbf{A})$，$\mathbf{P}_{b}=\mathbf{A}^{\mathbf{T}} /$rowsum$\left(\mathbf{A}^{\mathbf{T}}\right)$

此时的图卷积操作就变成：

$$\mathbf{Z}=\sum_{k=0}^{K} \mathbf{P}_{f}^{k} \mathbf{X} \mathbf{W}_{k 1}+\mathbf{P}_{b}^{k} \mathbf{X} \mathbf{W}_{k 2}$$

在本文中，提出一个自适应的邻接矩阵$\tilde{A}_{adp}$，即邻接矩阵是学出来的，并不是提前定义好的。

首先初始化2个节点嵌入矩阵$E_1,E_2 \in \mathbb{R}^{N \times c}$，

$$\tilde{\mathbf{A}}_{a d p}=\operatorname{SoftMax}\left(\operatorname{ReLU}\left(\mathbf{E}_{1} \mathbf{E}_{2}^{T}\right)\right)$$

通过上面的式子，可以得到自适应的邻接矩阵$\tilde{A}_{adp}$，下面定义图卷积层的操作。

1. 如果图的结构已知
参考DCRNN的扩散卷积的操作

• 无向图

  $$\mathbf{Z}=\sum_{k=0}^{K} \mathbf{P}^{k} \mathbf{X} \mathbf{W}_{k 1}+\tilde{\mathbf{A}}_{a p t}^{k} \mathbf{X} \mathbf{W}_{k 3}$$

• 有向图

  $$\mathbf{Z}=\sum_{k=0}^{K} \mathbf{P}_{f}^{k} \mathbf{X} \mathbf{W}_{k 1}+\mathbf{P}_{b}^{k} \mathbf{X} \mathbf{W}_{k 2}+\tilde{\mathbf{A}}_{a p t}^{k} \mathbf{X} \mathbf{W}_{k 3}$$

2. 图的结构未知

$$\mathbf{Z}=\sum_{k=0}^{K} \tilde{\mathbf{A}}_{a p t}^{k} \mathbf{X} \mathbf{W}_{k}$$

通过自适应的图卷积得到图中节点嵌入

3.2. 时间卷积层

使用1D空洞卷积TCN来捕获长期的时间依赖，因为空洞卷积可以扩大感受野的范围，可以捕获到更长的时间。同时，这里使用了门控TCN，

$$\mathbf{h}=g\left(\boldsymbol{\Theta}_{1} \star \mathcal{X}+\mathbf{b}\right) \odot \sigma\left(\boldsymbol{\Theta}_{2} \star \mathcal{X}+\mathbf{c}\right)$$

输入数据$\mathcal{X} \in \mathbb{R}^{N \times D \times S}$，$\star$表示1D空洞卷积操作。$g(\cdot)$使用Tanh激活函数。

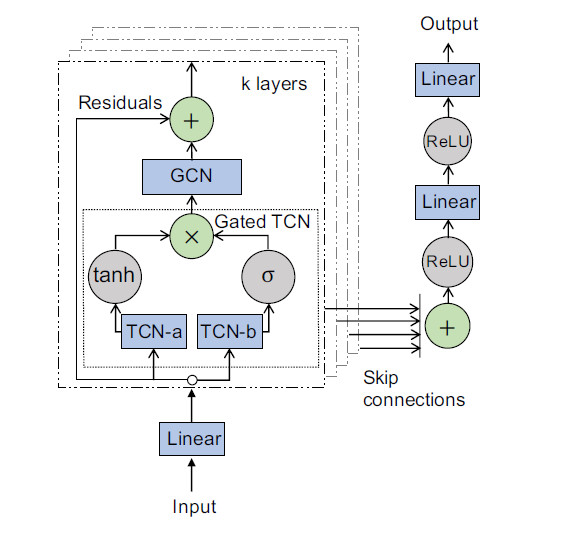
下面介绍模型的步骤

求自适应邻接矩阵—>T-GCN—>GCN

1. 首先模型的输入维度是(batch_size,D,N,T),首先经过$1*1$的2D卷积层，将节点特征D转换维度，变成(batch_size,D1,N,T)
2. 计算自适应邻接矩阵，首先初始化2个可学习的节点嵌入矩阵$\mathbf{E}_1,\mathbf{E}_2$,维度都是$\mathbb{R}^{N \times 10}$,然后使用下面的式子计算$\mathbf{A}_{adp}=F.softmax(F.relu(torch.mm(E1, E2)), dim=1)$

3. 将(batch_size,D1,N,T)输入到Gated-TCN中，首先输入到TCN-a（2D卷积当1D卷积用，卷积核中有1维为1）中，2D卷积的输入维度是D1，输出维度是D2，卷积核大小为(1,k)，然后再经过Tanh，输出维度(batch_size,D2,N,T)

   $$Tanh \left(\boldsymbol{\Theta}_{1} \star \mathcal{X}+\mathbf{b}\right)$$
4. 将(batch_size,D1,N,T)输入到TCN-b（2D卷积当1D卷积用，卷积核中有1维为1）中，2D卷积的输入维度是D1，输出维度是D2，卷积核大小为(1,k)，然后再经过Sigmoid，输出维度(batch_size,D2,N,T) $$\sigma\left(\boldsymbol{\Theta}_{2} \star \mathcal{X}+\mathbf{c}\right)$$
5. 将步骤3和步骤4的输出逐元素相乘 $$\mathbf{h}=Tanh \left(\boldsymbol{\Theta}_{1} \star \mathcal{X}+\mathbf{b}\right) \odot \sigma\left(\boldsymbol{\Theta}_{2} \star \mathcal{X}+\mathbf{c}\right)$$
6. 将步骤5的输出(batch_size,D2,N,T)，输入到skip-conv（1D卷积），改变通道维度为(batch_size,D3,N,T)存储在skip变量中，一共有K层，将K层G-TCN的输出加起来得到(batch_size,D3,N,T)

7. 下面进行GCN操作，将步骤5的输出(batch_size,D2,N,T)=x，假设有2个邻接矩阵，一个是已知的邻接矩阵$\mathbf{P}$,一个是自适应邻接矩阵$\mathbf{A}_{a p t}$，先遍历第一个邻接矩阵，$\mathbf{P}X$保存取来，然后在$\mathbf{P}^2X$，直到$\mathbf{P}^kX$，然后再求$\mathbf{A}_{a p t}X,\mathbf{A}_{a p t}^2X,\mathbf{A}_{a p t}^kX$。一共有2个邻接矩阵，每个邻接矩阵都有K个值，将这2K个值在通道维上拼接，得到$(batch_size,2KD2,N,T)$，然后在经过一个全连接，将维度映射成D1，即(batch_size,D1,N,T)

   $$\mathbf{Z}=\sum_{k=0}^{K} \mathbf{P}^{k} \mathbf{X} \mathbf{W}_{k 1}+\tilde{\mathbf{A}}_{a p t}^{k} \mathbf{X} \mathbf{W}_{k 3}$$

8. 将步骤7的输出和步骤1的输出做残差连接，直接相加，再经过一个BN层，完成一个block。接下来就再次经过G-TCN和GCN，重复步骤3-7

9. 所有的block完成之后，输出维度(batch_size,D1,N,T),但我们并不是要GCN的输出，而是需要每个TGCN的输出保存在skip中，维度(batch_size,D3,N,T)，先使用ReLU激活，然后使用$1 \times 1$的2D卷积，变成维度(batch_size,D4,N,T),再ReLU，然后是$1 \times 1$卷积