AUC在推荐系统中的应用

发表于 | 分类于 | 浏览 次
字数统计: 892 | 阅读时长 ≈ 3

参考资料

在推荐、广告系统中AUC是一个常见的指标。

1. 介绍AUC

深入理解AUC

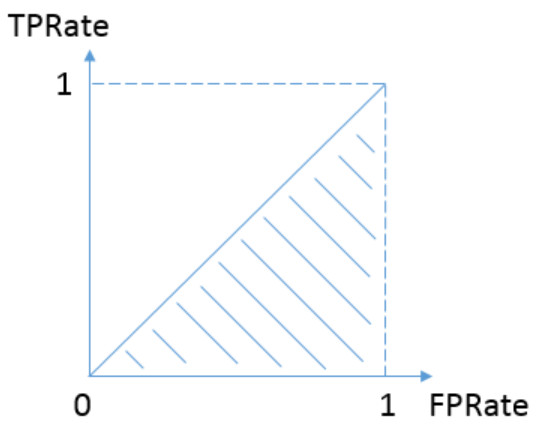
关于AUC，通常说是ROC线下面积。ROC横坐标假阳率，纵坐标真阳率。
如下图中AUC=0.5，表示不论样本真实label是0还是1，模型将以0.5的概率将其预测为正样本。这就和抛硬币没区别，这说明模型对正负样本没有区分能力。
我们训练的目标是让AUC越大越好。

在统计和机器学习中，常用AUC来评估二分类模型的性能。AUC全称是Area Under the Curve。

AUC同时考虑了分类器对正例和负例的分类能力，在样本不均衡时，分类器依然能做出合理的评价。

另一种解释是：基于概率的解释，评估模型的排序能力。

2. 排序问题中的AUC

假如AUC=0.7，表示给定一个正样本和一个负样本，在70%的情况下，模型对正样本的打分高于负样本的打分。可以看出，我们只关心正负样本之间的分数高低，并不在乎具体的概率值。

对于Precision，Recall等指标，AUC只关注排序结果，不关注模型输出的概率值，所以适合排序业务。
正负样本被预测的gap越大，AUC越大。

3. AUC的计算

将测试样本得到的概率从小到大排序，对于第$j$个正样本，假设它的排名是$r_j$，那就说明在这个正样本之前有$r_j-1$个样本，其中正样本个数为$j-1$个（因为这个正样本在所有正样本中排第j），那排在第j个正样本前面的负样本个数有$(r_j-1-(j-1))=r_j-j$个，也就是说，低于第$j$个正样本来说，其得分比随机取的一个负样本大（正样本的排名靠后）的概率是$\frac{r_j-j}{N_-}$,其中$N_-$是标签中负样本的个数，所以平均下来，随机取的正样本得到比负样本大的概率为：

即需要求出以下3个值：

  1. 所有正样本的排名，排名相加$\sum_{j=1}^{N_+}r_j$
  2. label中正样本个数$N_+$
  3. label中负样本个数$N_-$

$prob=[0.4,0.5,0.2,0.8,0.7,0.9,0.6]$
$label=[0^{0.4},0^{0.5},1^{0.2},1^{0.8},1^{0.7},0^{0.9},1^{0.6}]$

首先对prob从小到大排序，并同时调整prob的顺序
$prob=[0.2,0.4,0.5,0.6,0.7,0.8,0.9,]$
$label=[1^{0.2},0^{0.4},0^{0.5},1^{0.6},1^{0.7},1^{0.8},0^{0.9}]$

其中正样本的排名分别是1,4,5,6，排名相加是16。
label正样本个数有4个，负样本个数有3个，

$AUC=\frac{16-45/2}{43}=0.5$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def calAUC(prob,labels):
    f = list(zip(prob,labels))
    #按照prob从小到大排序，对labels进行排序
    rank = [cur_label for cur_pro,cur_label in sorted(f,key=lambda x:x[0])]
    #找出正样本在排名
    rankList = [i+1 for i in range(len(rank)) if rank[i]==1]
    posNum = 0#正样本的个数
    negNum = 0#负样本的个数
    for i in range(len(labels)):
        if(labels[i]==1):
            posNum+=1
        else:
            negNum+=1
    auc = 0
    auc = (sum(rankList)- (posNum*(posNum+1))/2)/(posNum*negNum)
    print(auc)
    return auc


if __name__ == "__main__":
    prob=[0.4,0.5,0.2,0.8,0.7,0.9,0.6]
    label=[0,0,1,1,1,0,1]
    calAUC(prob,label)
打赏
0%