RiskOracle-A Minute-level Citywide Traffic Accident Forecasting Framework

AAAI2020原文链接：RiskOracle-A Minute-level Citywide Traffic Accident Forecasting Framework
中国科大一个团队发表

• 1. 摘要
• 2. 介绍
• 贡献
• 3. 问题定义
• 4. Minute-level Real-time Traffic Accident Forecasting
  • 4.1. Framework Overview
  • 4.2. Data Preprocessing
  • 4.3. Multi-task DTGN for Accident Risk Prediction
• 5. 实验
  • 5.1. 数据准备
  • 5.2. 实现细节
  • 5.3. 评价指标
  • 5.4. Baseline
  • 5.5. 实验结果
  • 5.6. 超参数
  • 5.7. 案例分析
• 6. 总结
• 7. 知识补充

论文总结：

1. 根据网格构建图，将NYC划分了27*27个网格，但是其中只有354个网格有道路，所以图中有354个节点。
2. 根据网格之间道路相似性和历史一周交通的动态相似性来构建图中边的权重。构建的是全连通图，计算任意2个子区域的相似性
3. 多任务学习。主任务：预测m个子区域的risk，辅助任务1：预测m个子区域的flow，辅助任务2：预测q个中等区域的事故次数count
4. 在训练时，将risk=0替换为对应的负值，使用全部的数据。在测试时，只计算高频时间段和高频区域的评价指标

1. 摘要

    实时交通事故预测对公共安全和城市管理意义重大（例如，实时路径规划和应急响应部署）。之前的事故预测是在小时级别上，利用神经网络和静态的区域关系。然而，随着道路网络的高度动态性和交通师傅的稀有性，提高预测的粒度仍然是一个挑战，这将会导致结果偏差和零膨胀问题。在这篇论文中，我们提出一个新颖的RiskOracle框架，提高预测的粒度到分钟级别。具体来说，我们首先将0风险值转换为适合网络训练的值，然后，我们提出差分时变图神经网络(DTGN)来捕获交通状态的即时变化和子区间之间的动态相关性，并且，我们采用多任务和区域选择方案来突出显示全市范围内最可能发生事故的子区域，弥合了偏差的风险值和稀疏的事故分布。在2个真实数据集上做了大量实验证明了我们的RiskOracle框架的有效性和可扩展性。

2. 介绍

    交通事故预测对城市安全非常重要。构建一个细粒度级的事故预测模型，为乘客提供及时的安全路径规划，为新兴应用(智能交通和自动驾驶)提供准确的应急响应的需求越来越大。
    关于事故预测周期的长短，现有的工作主要分为2类：长期（天级别预测）和中期（小时级别预测）。我们在表1中总结了所有相关的工作。即使最近关于天级别的预测模型通过建模时空异质数据取得了很好的效果，但是对于紧急的情况并没有意义。
    在小时级别上的中期事故预测可以进一步划分为：传统方法和深度学习。传统方法包括：基于聚类，基于频率树，基于非负矩阵分解。但是，这些方法忽略了时间关系，不能建模复杂非线性的时空关系。深度学习方法例如，仅仅将历史交通事故数据输入到模型中，利用LSTM学习时间相关性，缺少了多源实时交通数据，效果不好。还有一些工作利用深度学习框架SDAE/SDCAE和ConvLSTM，结合人类实时移动数据，来学习交通事故模式，但是它们都不能提取区域间和区域内随时间变化的关系。
    即使深度学习模型的进展为小时级别的事故预测带了可喜的结果，但是我们认为其忽略了3个重要的问题，使得在分钟级别的预测效果较差。第一，在2019中提到的，当预测任务的时空分辨率提高时，会出现零膨胀问题，将预测所有的结果都为0。由于没有方法来解决这个问题，稀少的非零值在训练时使模型无法生效。第二，尽管CNN可以学习静态的子区域相关性，但是随时间变化的子区域相关性在城市短期事故预测有着重要的作用，例如，由于潮汐流，2个子区域在早上相关性强，在下午相关性弱。第三，在同一子区域相邻时间段内交通状况的异常变化通常会诱发交通事故或其他事件。没有考虑以上3个时空因素，小时级别的预测模型能力将受到严重阻碍。

表中的论文
Learning Deep Representation from Big and Heterogeneous Data for Traffic Accident Inference(2016AAAI)

A Deep Learning Approach to the Citywide Traffic Accident Risk Prediction(2018IEEE-ITSC)

Hetero-ConvLSTM: A Deep Learning Approach to Traffic Accident Prediction on Heterogeneous Spatio-Tem(2018KDD)

    这篇论文，我们研究了分钟级别的全市交通事故预测，提出了三阶段RiskOracle框架，该框架基于多任务差分时变图卷积(Multi-task DTGN)。三个阶段分别是：数据预处理阶段，训练阶段，预测阶段。在数据预处理阶段，我们提出一个感知策略以最大程度地推断全球交通状况，然后设计基于数据增强的先验知识来解决短期预测中的零膨胀问题。在训练阶段，我们提出Multi-task DTGN，其中时变总体上建模了短期子区域的动态相关性，差分特征生成器在交通状态即时变化和交通事故之间建立了高级联系。正如我们所知，交通事故和交通量在城市中通常分布不均衡，因此多任务方案旨在解决事故预测中的空间异质性，然后在预测阶段，我们利用学到的多尺度事故分布，获取到一组离散的最可能发生事故的子区域。在2个真实数据集上的实验证明了我们的框架在10-min和30-min级别的预测任务上都超过了state-of-the-art。

贡献

• 提升实时事故预测的时间粒度，从小时—>分钟
• 提出多任务STDN来解决短期事故预测的挑战。这是第一篇使用图卷积来解决事故预测问题
• 距离远但是有潜在关系的区域在图中可以被动态连接
• 通过差分特征生成器，交通状况的异常变化可以被捕获
• 多任务学习用来解决稀疏和空间异质性问题。多尺度的事故分布可以突出强调最可能发生交通事故的子区域
• 提出数据增强策略来解决零膨胀问题
• 提出协同感知策略来处理稀疏的感知数据

3. 问题定义

    在这一节，介绍基本定义，使用公式定义问题。
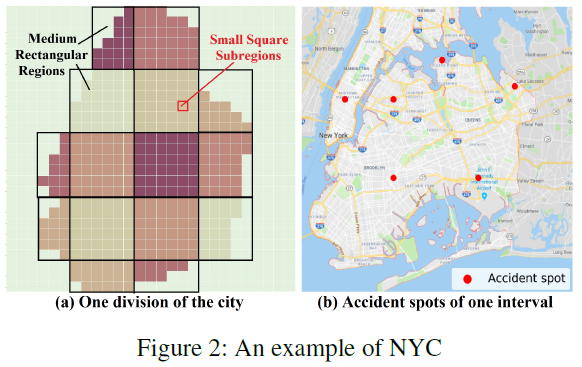
    在我们的工作中，如果直接将整个研究区域作为方形区域，使用CNN进行时空特征提取，尤其在实时事故预测中，则会导致不必要的冗余，因为城市轮廓通常是不规则的。如图2(a)所示，我们首先将路网中研究区域划分为q个中等大小的矩形区域，每一个矩形区域包含一些小的方形子区域。一共有m个子区域(subregion)，我们通过城市图对m个子区域建模。

定义1：Urban Graph：研究区域可以定义成无向图，用$G(\mathcal{V},\mathcal{E})$表示。顶点集$\mathcal{V}=\{v_1,v_2,…,v_m\}$，其中$v_i$表示第$i$个方形子区域，给定2个节点$v_i,v_j\in \mathcal{V}$,边$e_{ij} \in \mathcal{E}$表示2个subregion的连接，边非0即1。

$$e_{i j}=\left\{\begin{array}{ll}{1} & {\text { if the traffic elements within two }} \\ {} & {\text { subregions have strong correlations }} \\ {0} & {\text { otherwise }}\end{array}\right.$$

上面邻接矩阵的定义只是为了图定义的完整性，本文用到的邻接矩阵并不是非0即1的

    在该论文中，1个节点的traffic element包括2方面，静态的道路特征和动态的traffic特征。$\rho$来控制affinity matrix$\mathcal{A}_s$和$\mathcal{A}^{\Delta t}_o$的稀疏性，表示整个urban graph的连通性，在affinity matrix中的非0值表示subregion之间有很强的相关性。
    在一个时间段$\Delta t$中subregion $v_i$的动态traffic特征包括3部分，(a)人流量，用traffic volume$TV_{v_i}(\Delta t)$表示;(b)交通状况，用平均交通速度$a_{v_i}(\Delta t)$表示;(c)交通事故风险等级$r_{v_i}(\Delta t)$。

定义2：Static Road Network Features：一个城市subregion节点$v_i \in \mathcal{V}$,它的静态路网特征包括道路个数，道路类型，道路长度和宽度，除雪等级，红绿灯个数，subregion $v_i$中的所有道路使用一个固定长度的向量$s_i$表示。整个urban graph的静态道路特征使用$S=\{s_1,s_2,…,s_m\}$表示。静态特征，不随着时间变化，没有时间下标。

定义3：Dynamic Traffic Features：对一个subregion节点$v_i \in \mathcal{V}$,在时间段$\Delta t$中，它的动态交通特征被表示为$f_{v_i}(\Delta t)=\left\{T V_{v_{i}}(\Delta t), a_{v_{i}}(\Delta t), r_{v_{i}}(\Delta t)\right\}$，即该时间段的车流量，车平均速度，事故风险，$r_{v_i}(\Delta t)$是交通事故的risk求和，将交通事故分为3类：轻度，中度，重度，risk值分别是1,2,3.所有子区域在时间段$\Delta t$的交通事故风险分布表示为$\mathcal{R}(\Delta t)=\left\{r_{v_{1}}(\Delta t), r_{v_{2}}(\Delta t), \cdots, r_{v_{m}}(\Delta t)\right\}$，动态交通特征表示为$\mathcal{F}(\Delta t)=\left\{f_{v_{1}}(\Delta t), f_{v_{2}}(\Delta t), \cdots, f_{v_{m}}(\Delta t)\right\}$。动态交通特征随着时间变化，所以有区域和时间2个变量，动态特征包括：人流量，交通平均速度，事故风险

定义4:Traffic Accident Prediction：给定所有子区域的静态道路特征$S$和所有子区域历史$T$个时间段的动态交通特征$\mathcal{F}(\Delta t)(\Delta t=1,2,…,T)$,目标是预测下一个时间段全市的事故风险$\mathcal{R}(T+1)$和选出高风险的子区域$\mathcal{V}_{acc}(T+1)$

总结：根据m个子区域构建无向图，节点表示子区域，边表示2个子区域特征之间的相关性。子区域的特征包括2类：静态道路特征和动态交通特征。静态道路特征包括：道路个数，道路类型，长宽，道路除雪等级，红绿灯个数。动态交通特征包括：在该时间段内的车流量，车平均速度，该子区域事故风险。

4. Minute-level Real-time Traffic Accident Forecasting

    在这一节，先整体看一下我们的RiskOracle框架，然后再详细介绍。

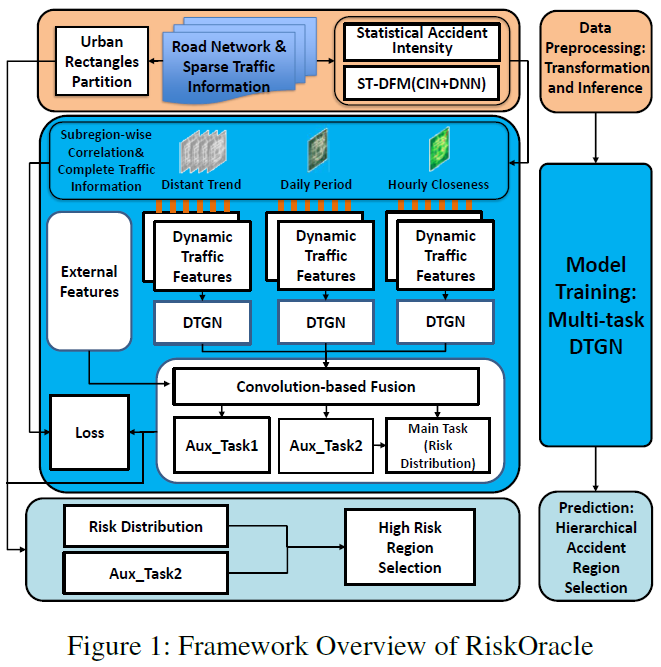
4.1. Framework Overview

    如图1所示，RiskOracle框架包括3个阶段：数据预处理阶段，训练阶段，预测阶段。

4.2. Data Preprocessing

解决事故预测中的空间异质。高风险的值通常出现在城市区域，由于市中心发生事故多且车流量大，导致风险值在空间上不均衡，会忽略农村地区相对高风险的区域。为了实现全市预测，选择最有可能发生事故的区域来解决空间异质性是非常必要的。如图2(a)所示,按照层次结构组织这个子区域，中等大小区域用来收集粗粒度的事故分布，小的子区域用来收集细粒度的事故分布，然后进一步突出显示每个中等区域中的子区域。多尺度分布也可以看做分层事故分布。
解决零膨胀问题。深度神经网络在训练中，如果非零值非常少的话，受到零膨胀的影响，将会预测出无效的值。如图2(b)所示，在选定的10min中，整个NYC只有6个交通事故，说明在短期事故的内在稀有性。为了解决这个问题实现实时事故预测，我们设计基于先验知识的数据增强(PKDE)策略来区分训练数据集中标签的风险值。具体来说，对时间段$\Delta t$,我们将所有区域在该时间段内的风险值$\mathcal{R}(\Delta t)$中的0转换为具有区分度的负值。转换分为2步：a)风险中的0值通过等式2转换为事故风险指标；b)指标值通过等式3转换为静态事故强度。给定子区域$v_i$，我们计算它的事故风险指标$\varepsilon_{v_i}$ ，事故风险指标是个比例值，在[0,1]之间

$$\varepsilon_{v_{i}}=\frac{1}{N_{\text {week}}} \sum_{j=1}^{N_{\text {week}}} \frac{r_{v_{i}}(j)}{\sum_{k=1}^{m} r_{v_{k}}(j)}$$

其中$N_{week}$是训练集中总共的周数，$r_{v_{i}}(j)$是区域$v_i$在第$j$周总的风险值。然后，根据该子区域的事故风险指标$\varepsilon_{v_i}$,我们通过以下公式计算子区域$v_i$的统计事故强度。

$$\pi_{v_{i}}=b_{1} \log _{2} \varepsilon_{v_{i}}+b_{2}$$

总结：给定时间段$\Delta t$，将子区域中的riks 0值转换为负值，先计算事故风险指标，再计算事故强度。有m个子区域，每个子区域都有一个固定的事故强度，将该子区域risk=0值用该子区域的事故强度替换

其中$b_1$和$b_2$是算子，用来保持绝对值$\pi_{v_{i}}$的范围和真实风险值的范围对称。我们通过对数在0和1之间的区分性质，可以使转换后的数据易于区分并适合于训练网络。转换的方式为：1)事故风险为0的子区域的事故强度为负，小于非零风险的子区域，反映了零风险子区域有较低的事故风险;2)具有较低事故风险指标的子区域有较低的事故概率，保留了实际事故风险的等级。
事故风险指数$\varepsilon_{v_{i}}$值在[0,1]之间，取对数值在$(-\infin,0]%$，如果一个子区域的风险值为0，则事故风险指数为0，则事故强度$\pi_{v_{i}}$为负。

其中b1和b2的值是反复试出来的。为了保证事故强度的绝对值和真实风险范围对称。假设真实风险在1至25之间，那事故强度的值要在-25至-1之间，通过设置b1和b2强度值在-25~-1

补充稀疏的传感数据。实时交通信息的通常收集不足来进行事故预测，动态交通信息通常和静态空间路网结构相互影响，因此，我们提出了一个协同感知策略，利用FM的交互操作，修改xDeepFM为时空深度因式分解(ST-DFM)。

我们首先通过静态关联矩阵$\mathcal{A}_s$来提取2个子区域间的路网相似性和连接性。其中关联矩阵affinity matrix中的元素$\alpha_s(i,j)$表示子区域$v_i和v_j$间的静态相关性。

$$\alpha_{s}(i, j)=\left\{\begin{array}{cc} {1} & {\text { if subregion } v_{i} \text { and }} {v_{j}} {\text { are adjacent }} \\ {e^{-J S\left(s_{i} \| s_{j}\right)}} & {\text { otherwise }} \end{array}\right.$$

其中，$JS$函数是Jensen-Shannon divergence（散度），$s_{i}和s_{j}$是子区域$i,j$的静态道路特征，包括道路个数，类型，长宽，除雪等级，红绿灯个数。

$$J S\left(s_{i} \| s_{j}\right)=\frac{1}{2} \sum_{k}\left(\begin{array}{c} {s_{i}(k) \log \frac{2 s_{i}(k)}{s_{i}(k)+s_{j}(k)}+} \\ {s_{j}(k) \log \frac{2 s_{j}(k)}{s_{i}(k)+s_{j}(k)}} \end{array}\right)$$

和xDeepFM一样，ST-DFM包含压缩交互网络模块和DNN模块。在ST-DFM中嵌入了3个时空字段，即静态空间特征，动态交通特征和时间戳。然后ST-DFM通过CIN模块学习矢量级别不同时空特征间的交互关系，通过DNN模块学习特征的高级表示，最后获取高级特征的组合。我们将对应子区间的交通量输入到ST-DFM中来推断速度值，反之亦然。然后通过训练2个实时交通数据的交集数据，来最大程度推断交通信息，以此获取全局交通状态。

补充：JS散度是一个衡量距离的函数，JS散度的值域在[0,1]之间，相同为0，反之为1。静态affinity matrix $\mathcal{A}_s \in R^{m \times m}$，如果2个子区域相邻，值为1，不相邻则计算2个子区域的静态道路特征的相似度，值在$[\frac{1}{e},1]$之间，越相似，值越靠近1，越不相似，值越靠近$\frac{1}{e}$
通过静态道路特征构建一个全连接图，任意2个节点都有边相连，只是权重不同。如果2个子区域相邻，边权重为1，如果子区域不相邻，计算2个子区域间的JS散度

4.3. Multi-task DTGN for Accident Risk Prediction

时空DTGN.事故和交通拥堵在路网中通常相互影响，特别是节假日和高峰。由于GCN对非欧式空间很好的建模，我们提出了DTGN，通过time-varying overall affinity和differential feature generator来修改GCN，解决分钟级别预测事故的挑战。

Time-varying overall affinity matrix with dynamic traffic features involved. 不同城市分区之间的交通状况有很强的时变相关性。并且，交通事故和交通状况有很强的时空相关性。因此，对于分钟级别的事故预测，需要通过动态affinity matrix $\mathcal{A}^{\Delta t}_o$捕获子区域间在时间段$\Delta t$的时间交通相关性。在$\mathcal{A}^{\Delta t}_o$中的元素$\alpha^{\Delta t}_o(i,j)$表示子区域$i,j$的动态相似性。

$$\alpha_{O}^{\Delta t}(i, j)=e^{-J S\left(s_{i}^{*} \| s_{j}^{*}\right)}+\gamma * e^{-J S\left(C_{i}^{\Delta t} \| C_{j}^{\Delta t}\right)}$$

其中$C_{i}^{\Delta t}$表示子区域$v_i$上周每一天相同时间段的交通量$TV_{v_i}(\Delta t)$和平均速度$a_{v_i}(\Delta t)$。注意我们使用Attention机制，根据子区域的静态空间特征对事故的影响，修改了子区域静态空间特征的权重。并且子区域的静态特征表示为$s^*_i$.权重$\gamma$用来调节动态交通affinity占overall affinity matrix的比例。通过overall affinity matrix，距离较远但有潜在事故相关的子区域可以被动态连接。为了在谱域运行GCN，我们需要计算动态affinity matrix $\mathcal{A}^{\Delta t}_o$的拉普拉斯矩阵$L^{\Delta t}$，其中$\mathcal{A}^{\Delta t}_o$可以被看做邻接矩阵。首先定义$\mathcal{B}^{\Delta t}$

$$\mathcal{B}^{\Delta t}=\mathcal{A}_{o}^{\Delta t}+I_{m}$$

其中$I_{m}$是维度$m \times m$的单位矩阵。然后计算度矩阵$\Phi^{\Delta t}$

$$\Phi^{\Delta t}=\left[\begin{array}{cccc} {\varphi_{11}} & {0} & {\cdots} & {0} \\ {0} & {\varphi_{22}} & {\cdots} & {0} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {0} & {0} & {\cdots} & {\varphi_{m m}} \end{array}\right]$$

其中$\varphi_{i i}=\sum_{j=1}^{m} b_{i j}$，将矩阵$\mathcal{B}^{\Delta t}$每一行的元素相加组成度矩阵。然后获取时间段$\Delta t$的拉普拉斯矩阵。

$$L^{\Delta t}=\left(\Phi^{\Delta t}\right)^{-\frac{1}{2}} \mathcal{B}^{\Delta t}\left(\Phi^{\Delta t}\right)^{-\frac{1}{2}}$$

补充：原始GCN中，拉普拉斯矩阵为$\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$，其中$\hat{A}=A+I$

总结：文中提到的affinity matrix有2类：静态affinity matrix $\mathcal{A}_s$和动态overall affinity matrix $\mathcal{A}_o^{\Delta t}$，这2个矩阵的维度都是$R^{m \times m}$，其中静态affinity matrix不随着时间变化，根据子区域的静态道路特征计算得到。动态overall affinity matrix随着时间变化，由子区域的静态道路特征和上周每一天同时间段的动态交通特征(车流量和车平均速度)计算得来。这里将动态overall affinity matrix看做邻接矩阵，计算拉普拉斯矩阵，每个时间段都有一个拉普拉斯矩阵，用在GCN中。

Differential GCN for extracting spatiotemporal features和常规的交通状况相比，事故或事件预测和交通状况的异常变化更相关。因此，我们引入了差分特征生成器来计算相邻时间段的差分图片。将差分动态交通特征输入到GCN中，可以对交通状况的异常变化的传播和相互作用进行建模，并且可以学习即时的交通状态变化和事故之间的高层关系，可以更好地用来分钟级的事故预测。给定时间段$\Delta t$,差分向量$\vec{\Theta}^{\Delta t}$计算如下：

$$\vec{\Theta}^{\Delta t}=\mathcal{D}(\Delta t)-\mathcal{D}(\Delta t-1)$$

其中$\mathcal{D}(\Delta t)=\left\{d_{v_{1}}(\Delta t), d_{v_{2}}(\Delta t), \cdots, d_{v_{m}}(\Delta t)\right\}$,$d_{v_{i}}(\Delta t)=\left\{T V_{v_{i}}(\Delta t), a_{v_{i}}(\Delta t)\right\}$，差分不涉及到事故风险的计算。在时间段$\Delta t$中所有的子区域通过结合它们的动态交通特征和对应的差分向量，生成了统一的特征元组$\mathcal{U}(\Delta t)=\left\{\mathcal{F}(\Delta t), \vec{\Theta}^{\Delta t}\right\}$,在郑宇AAAI2017 ST-ResNet文中提到的，城市交通有3个时间周期：小时，天，长期趋势。所以，预测时间段$\Delta t$，我们选取$\mathcal{k}$个统一特征元组，按照ST-ResNet，设置$\mathcal{k}=3$,作为DTGN的输入。具体来说，选取时间段$\Delta t$的前$\mathcal{k}$个时间段作为小时周期，选取连续前$\mathcal{k}$天中相同的时间段作为天周期，至于长期趋势，向前每10天取1天，一共取$\mathcal{k}$天,在这$\mathcal{k}$天种，取相同的时间段作为长期趋势。即hour周期有$\mathcal{k}$个时间段,天周期有$\mathcal{k}$个时间段，长期区域有$\mathcal{k}$个时间段。如图1所示，将这3个时间周期的二元组分别输入到3个DTGN中。其中DTGN的模型细节在图3(a)中。对于每一个时间周期，将它的特征二元组用$\mathbb{U}_{} \Delta t$表示，将$\mathbb{U}_{} \Delta t$输入到FCN中，将特征嵌入成低维特征，然后输入到GCN中。

$$\mathcal{H}^{n+1}=\text{Leaky-ReLU}(L^* \mathcal{H}^{n} \mathcal{W}^{n}),\text { where } \mathcal{H}^{0}=\mathbb{U}_{*}^{\Delta t}$$

其中$\mathcal{H}^{n}$表示第n层GCN输入的特征，$\mathcal{W}^{n}$表示第n层GCN的卷积核参数。因为每个时间周期会输出多个时间段的数据，在做GCN操作时，需要用到拉普拉斯矩阵，这里的$L^*$是输入所有时间段的拉普拉斯矩阵$L^{\Delta t}$的平均。每2个GCN后使用1次BN，防止梯度爆炸。考虑到转换后的risk中有负值，使用Leaky_ReLU激活。同时，对应时间段的外部数据(时间戳和天气)经过嵌入层变成定长的向量，再和GCN的输入融合。因为有3个时间周期，DTGN有3个输出，分别用$\mathcal{O}_{h c}^{\Delta t}, \mathcal{O}_{d p}^{\Delta t}$ and $\mathcal{O}_{d t}^{\Delta t}$表示。

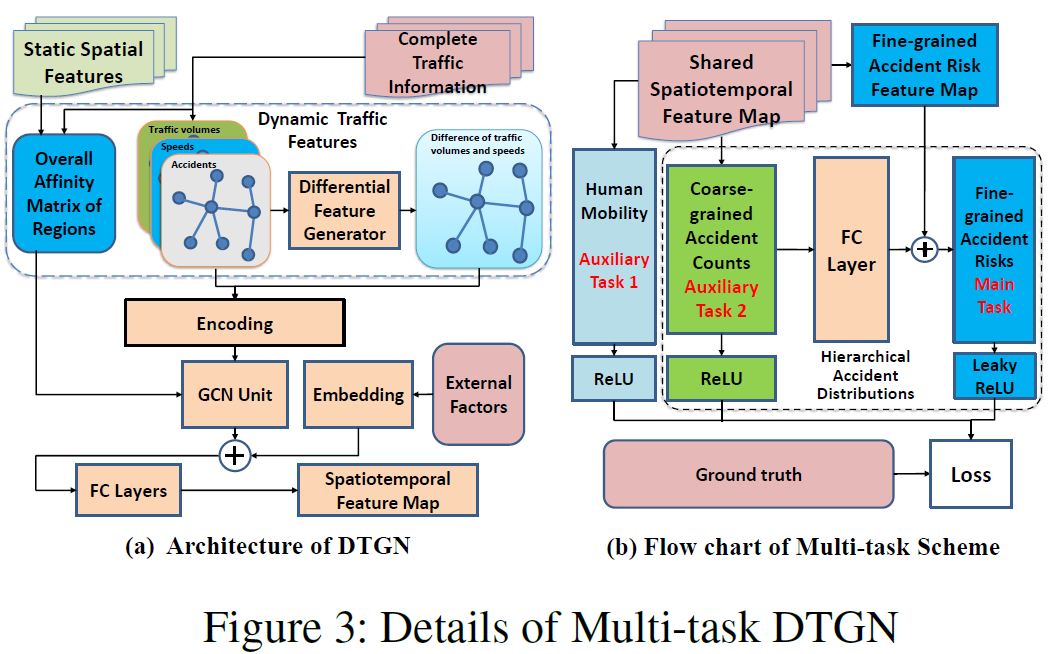
总结：每一个时间段有一个差分向量，是该时间段所有区域的车流量和车平均速度减去上一时间段的值，得到差分向量。然后将该时间段所有子区域的动态交通特征$\mathcal{F}(\Delta t)$和该时间段的差分向量$\vec{\Theta}^{\Delta t}$组成一个统一的特征元组$\mathcal{U}(\Delta t)$。那么每个时间段都有一个特征元组，存储所有子区域的特征。受郑宇2017AAAI ST-ResNet的启发，事故的发生有小时，天，长期的周期性，假设预测时间段是t，为其找出小时，天，长期的时间段。小时周期：[t-1,t-2,t-3]，天周期：[昨天t,前天t,大前天t]，长期周期[10天前t,20天前t,30天前t],然后分别输入到3个DTGN中。这个拿1个DTGN举例。输入的图信号矩阵维度是(batch_size,N,TD)=(batch_size,N,3\5)将时间维度乘到特征上，先经过FCN对特征进行嵌入，变成低维特征。然后输入到GCN中，GCN操作需要使用拉普拉斯矩阵。上节中提到拉普拉斯矩阵是动态的，每一个时间段都有一个L，这里每个周期都有3个时间段，使用的拉普拉斯矩阵是3个时间段拉普拉斯矩阵的平均值。
预测第t时间段的risk，输入的图信号矩阵：
小时周期：
t-1,t-2,t-3时刻：车流，车速，risk，$\Delta$车流，$\Delta$车速
天周期：
昨天t，前天t，大前天t时刻：车流，车速，risk，$\Delta$车流，$\Delta$车速
周周期：
10天前t，20天前t，30天前t时刻：车流，车速，risk，$\Delta$车流，$\Delta$车速
一共有3个组件，每个组件输入的维度是(batch_size,N,3*5)
外部因素：被预测时间段的天气等

多任务学习来事故风险预测设计多任务学习方案，不仅可以增强深度学习的表示能力，还可以学到分层事故分布，为最可能发生事故区域的选取提供指导。为了预测子区域的事故风险，我们首先将事故风险分布作为主任务。考虑到交通事故和人类活动强度有关，我们将区域交通量预测作为第一个辅助任务，用来提高深度学习的表示能，。为了给分层事故区域的选取提供指导，将预测中等区域发生的事故总数作为第二个辅助任务。
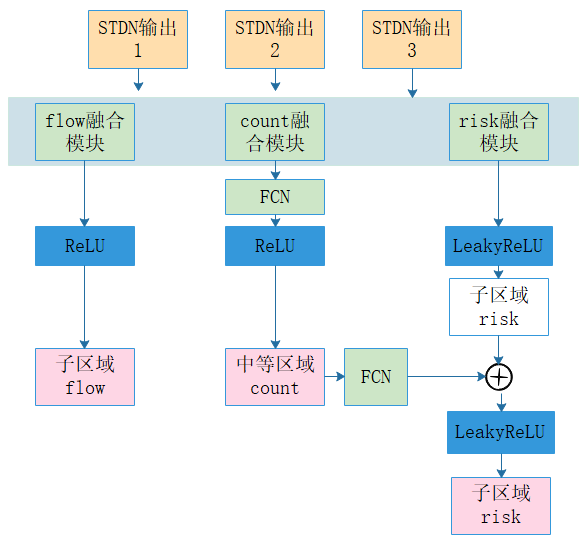
具体地，我们将DTGN的3个输出$\mathcal{O}_{h c}^{\Delta t}, \mathcal{O}_{d p}^{\Delta t}$ and $\mathcal{O}_{d t}^{\Delta t}$输入到卷积融合模块中，然后进行多任务学习，如图3(b)所示，3个多任务shared是3个DTGN的输出结果。将3个输出结果分别输入到3个融合模块中，3个融合模块的参数是$\mathcal{W}_{risk}^{\Delta t},\mathcal{W}_{vol}^{\Delta t},\mathcal{W}_{count}^{\Delta t}$，首先生成每个子区域的预测风险$\mathcal{O}_{\text {risk}}^{\Delta t}$,使用$Leaky_ReLU$激活是因为label中的risk值有负值，其余都使用$ReLU$激活。然后生成每个子区域的预测流量$\mathcal{O}_{v o l}^{\Delta t}$，然后预测每个中等区域的风险次数，先经过融合模块，再经过全连接，生成$\mathcal{O}_{\text {count}}^{\Delta t}$

$$\mathcal{O}_{r i s k}^{\Delta t}=\text { Leaky } \operatorname{ReLU}\left(\mathcal{W}_{risk}^{\Delta t} *\left[\mathcal{O}_{h c}^{\Delta t}, \mathcal{O}_{d p}^{\Delta t}, \mathcal{O}_{d t}^{\Delta t}\right]\right)$$ $$\mathcal{O}_{v o l}^{\Delta t}=\operatorname{ReLU}\left(\mathcal{W}_{v o l}^{\Delta t} *\left[\mathcal{O}_{h c}^{\Delta t}, \mathcal{O}_{d p}^{\Delta t}, \mathcal{O}_{d t}^{\Delta t}\right]\right)$$ $$\mathcal{O}_{\text {count}}^{\Delta t}=\operatorname{ReLU}\left(\mathcal{W}_{f c}^{\Delta t} *\left(\mathcal{W}_{\text {count}}^{\Delta t} *\left[\mathcal{O}_{h c}^{\Delta t}, \mathcal{O}_{d p}^{\Delta t}, \mathcal{O}_{d t}^{\Delta t}\right]\right)\right)$$

$\mathcal{O}_{\text {count}}^{\Delta t}$是中等区域的事故次数，将其输入到另一个全连接中，reshape成和$\mathcal{O}_{\text {risk}}^{\Delta t}$相同维度，和原先的细粒度事故分布相加，迫使学习粗粒度和细粒度的事故分布之间的关系。最终$\mathcal{O}_{\text {risk}}^{\Delta t}$被更新为

$$\mathcal{O}_{risk*}^{\Delta t}=\text { Leaky } \operatorname{ReLU}\left(\mathcal{W}_{f c *} * \mathcal{O}_{c o u n t}^{\Delta t}+\mathcal{O}_{r i s k}^{\Delta t}\right)$$

其中$\mathcal{O}_{risk*}^{\Delta t}$是最终主任务的输出。

多任务的总loss如下：

$$\operatorname{Loss}(\theta)=m s e_{r i s k}+\lambda_{1} * m s e_{v o l}+\lambda_{2} * m s e_{c o u n t}+\lambda_{3} * L_{2}$$

其中$m s e_{r i s k}, m s e_{v o l},m s e_{c o u n t}$是主任务和2个辅助任务的loss，这里使用L2正则化来避免过拟合。$\lambda_{1},\lambda_{2},\lambda_{3}$是损失函数的超参数。$\lambda_{1}=0.8,\lambda_{2}=1,\lambda_{3}=1e-4$。

只根据risk，count，flow的MSELoss进行反向传播，训练模型。在预测时，根据这3个输出，求出评价指标

分层最可能发生事故区域选择.交通事故和交通量在城市和农村经常不均衡，导致空间异质性问题。因此，用统一的风险阈值来选择最可能发生事故的区域是不合理的，我们基于多任务中预测出的risk，提出一个分层的最可能发生事故区域选择的方法。
输入数据是中等区域的事故次数和子区域的risk值，对每个中等区域$i$，我们从中选出$k_i(i=1,2,…,q)$个风险最高的子区域，其中参数$k_i$等于第二个辅助任务学到的$\mathcal{O}_{\text {count}}^{\Delta t}$中对应的值。因此，我们获得了一组最可能发生事故的子区域。并且通过这种方式获得的$k_i$可以减少区域的过度预测，并且模型符合时间和天气的变化。

对于$k_i$的选择这里解释下：在测试阶段，根据q个中等区域的事故数和m个子区域的risk值来选择$k_i$，假设q=5，预测出来5个中等区域发生的事故次数为[0,2,4,1,6],那就从5个中等区域中，分别选0,2,4,1,6个子区域，选risk最高的$k_i$个对应的子区域，就是模型预测的事故高发子区域

在模型训练阶段，只预测子区域的risk，子区域的flow，中等区域的count来计算loss，训练模型。在训练阶段，并不预测发生事故最高的区域。预测发生事故最高的区域，只在测试集上进行。在训练集和验证集上，将risk中的0替换掉训练模型，在测试集上，不需要将risk=0替换掉，因为在测试集上我们只需要找出topK就可以了。

5. 实验

分钟级别的事故预测模型，设置时间段分别为10min和30min

5.1. 数据准备

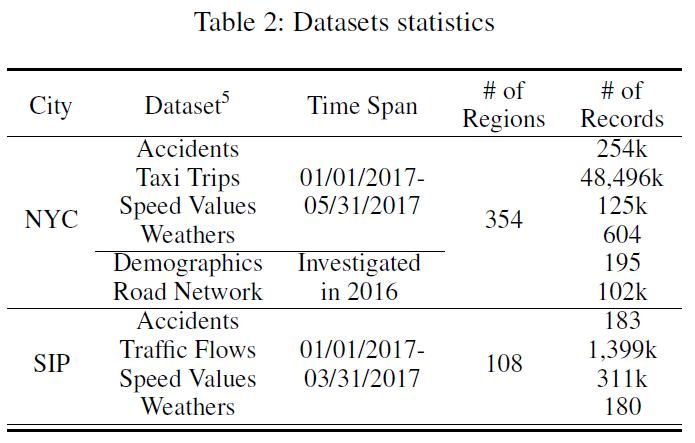
在2个真实数据集上做实验：NYC Opendata和苏州工业园区(SIP)。对于NYC数据集，由于缺少实时的交通流量数据，这里利用每个子区域的出租车流量来代表人流量。对于SIP数据集，它包含交通流量和速度。我们将其从新浪收集的交通事故数据集集成。2个数据集的统计信息在表2中。

5.2. 实现细节

训练集:验证集:测试集=6:1:3，划分子区域参照AAAI2019Spatiotemporal Multi-Graph Convolution Network for Ride-hailing Demand Forecasting和实际情况。堆叠9层GCN，每层有384个filter。损失函数中$\lambda_{1}=0.8,\lambda_{2}=1,\lambda_{3}=1e-4$。优化器使用Adam。

在训练阶段，动态交通数据和affinity matrix被划分为小时，天，长期共3组，2种scale的事故分布输入到多任务DTGN中。在测试阶段，将数据组织成以上格式并输入到模型中，最有可能发生事故的子区域可以从主任务和辅助任务2中得到。高风险子区域被突出显示，并与实际的事故记录比较。

5.3. 评价指标

从2个角度验证RiskOracle模型，回归角度：MSE，分类角度：a)Acc@M，常用于时空排名任务中，表示m个子区域中，预测的前M个风险最高的子区域中正确的比例。NYC数据集中，在30min预测时，M=20，在10min预测时，M=6。在SIP数据集中，M=5。b)Acc@K,其中K是第二个辅助任务学到的$k_i$的总和。其中Acc1表示发生事故频率较高时间段的准确率，例如早上7~9点，下午12~4点。

测试时，$Acc@M$：每个时间步从m个子区域中选出M个事故高发的区域，然后看选对了多少。M是全局选M个，每个中等子区域选多少个并不限制。$Acc@K$，只针对高频时间段计算该指标。假设在一个时间段中辅助任务2预测结果为[0,2,4,1,6],即K=13，从m个子区域中选出13个，但是每个中等子区域要选$k_i$个。

5.4. Baseline

1. ARIMA，用于时间序列预测
2. Hetero-ConvLSTM(2018KDD),调整超参数为4,blocks with 16 filters, and a size of 12x12 moving window with step=6.
3. ST-ResNet(2017AAAI郑宇)用来预测车流量
4. SDAE(2016AAAI)使用人流量来预测risk
5. SDCAE最新的小时级别风险预测模型

5.5. 实验结果

性能比较
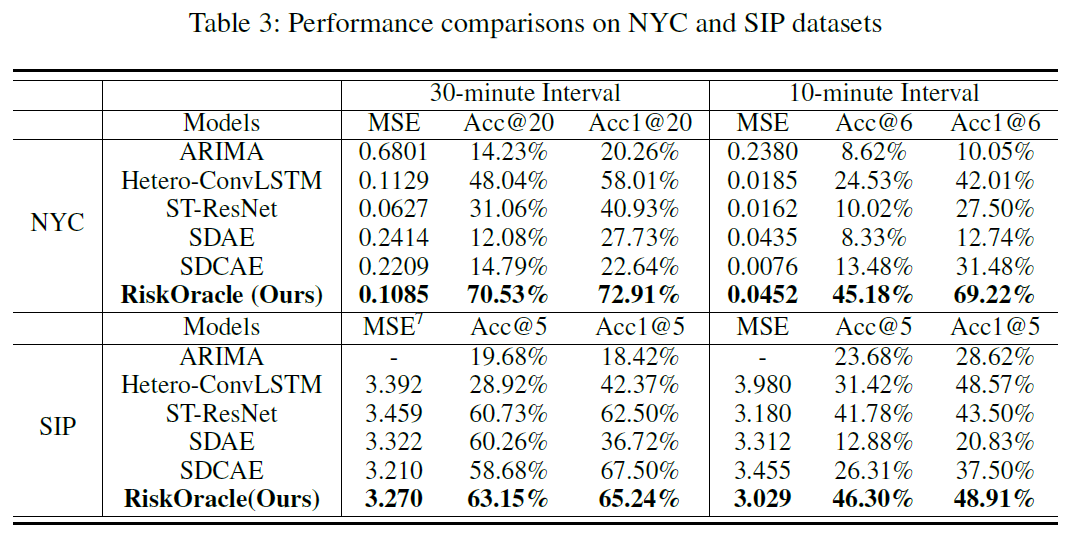
实验结果如表3.RiskOracle获得了最高的准确率，且MSE优于大部分baseline。使用分层事故区域选择HARS，我们的模型解决了空间异质性和过度预测的问题。尤其在NYC数据集上，我们模型在Acc@20比最好的模型高22.49%。对于稀疏的传感数据和短期的时空预测，可扩展性高。并且，我们的模型在高峰期的预测更好，在现实应用中有用。所有的指标NYC的都比SIP的要好，可能因为SIP数据中事故标签不完整。
总体上，随着时间粒度变小，我们的模型性能稍微下降，而其他的模型急剧下降因为遇到零膨胀问题。这表明我们的模型在短期事故预测中的有效性和可扩展性。在实际应用中有很少的事故记录时，2个数据集上的提升验证了我们模型的健壮性和普适性。

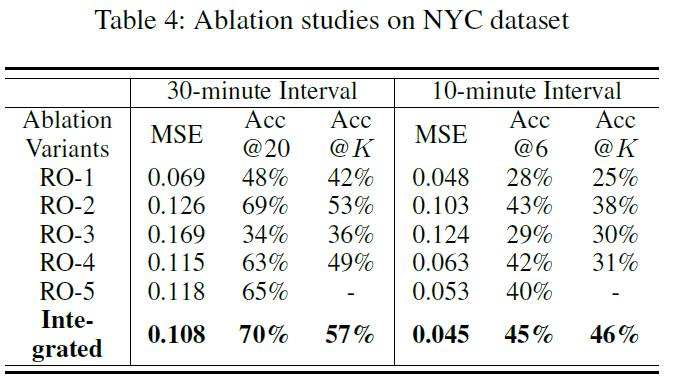
Acc@K和消融实验.如图4所示。Acc@20和Acc@6的结果略高于Acc@K，这是合理的，因为统一阈值无法适应实时条件，并且往往会高估事故率。相反，我们的框架具有使用多尺度事故分布预测，近似估计每个矩形区域中事故数量，具有灵活性。与表3中的结果相比，我们的框架胜过其他baseline，并在Acc@K达到可接受的准确性水平。
为了验证哪个组件起作用，做了消融实验，从模型中去掉一些组件。

• RO-1：去掉基于先验知识的数据增强PKDE，无法解决零膨胀问题。priori knowledge-based data enhancement
• RO-2：去掉ST-DFM，无法解决实时交通数据缺失问题
• RO-3：去掉overall affinity，无法实现时变的GCN,即图的邻接矩阵是静态的
• RO-4：去掉差分特征生成器，在输入到GCN中没有差分特征
• RO-5：去掉带有HARS的多任务
• Integrated model：完整模型
  其中最重要的组件是overall affinity和PKED，说明零膨胀和时变GCN是重要的。

5.6. 超参数

在NYC数据集的30min展示超参数实验。

• 9层GCN，每层有384个filter
• 损失函数中$\lambda_{1}=0.8,\lambda_{2}=1,\lambda_{3}=1e-4$
• 计算overall affinity时动态元素占的比重$\gamma=0.5$
• 中等区域个数$q=18$

5.7. 案例分析

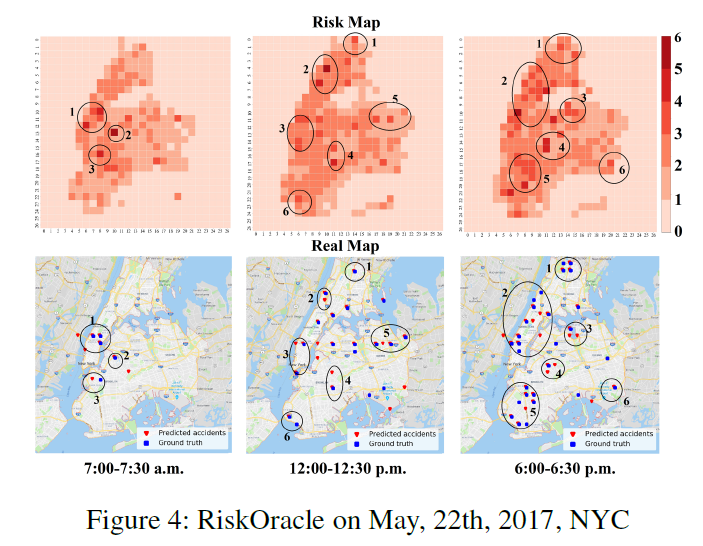
可视化NYC2017.5.22这一天中选取的3个30min时间段。上面是预测值，下面是真实值。可以看到预测的高风险子区域和真实值相似。由于在周日上午很少人外出，因此早晨7:00预测发生的事故很少。但是，下午事故数量会增加，而到了晚上，事故更加严重，由于当晚大雨，路况易发生事故。结果证明，辅助任务和HARS通过捕获外部因素，来学习事故分布的动态模式，调整推理，比统一阈值解决方案具有更好的适应性。

6. 总结

在这篇论文中，我们提出了基于多任务DTGN的RiskOracle框架，解决分钟级的事故预测问题。首先提出2个方法来解决零膨胀和稀疏感知的问题。在多任务DTGN中，结合差分特征生成器和时间overall affinity，模型可以建模稀疏的时空数据，捕获短期的子区域相关性。学习多尺度事故分布，突出显示最可能发生事故的子区域来解决空间异质性。在2个真实数据集上的实验验证模型的优越性。

7. 知识补充

【Factorization Machine】 FM (Factorization Machine) 主要是为了解决数据稀疏的情况下，特征怎样组合的问题。
【推荐系统】Factorization Machine