评价指标

发表于 | 分类于 | 浏览 次
字数统计: 1.4k | 阅读时长 ≈ 5

介绍在回归问题中的主要评价指标，以及各自的特点

1. 问题

在回归问题中，标签y的分布不均衡，范围在[1,88]，其中70%的值都在1左右。解决的方法：从损失函数入手，设计不同的评价指标，让其更关注一些大的y值。

2. 回归问题

Metircs参考资料

2.1. MAE(平均绝对误差)

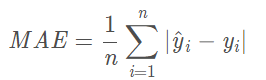
绝对误差的平均值。

  1. 范围在$[0,\infin]$
  2. 单看MAE并不能看出这个模型的好坏，因为不知道y的平均值。比如MAE=10,y的平均值为1000，则这个模型还不错，但是如果y的平均值为1，那这个模型就非常不好。
  3. 改进：$MAE/y_{mean}$

2.2. MSE(误差平方平均值)

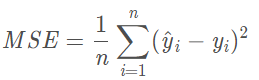
  1. 范围在$[0,\infin]$,
  2. 很多算法的loss函数都是基于MSE的，因为MSE计算速度快，比RMSE更容易操作。但是我们很少把MAE作为最终的评价指标。
  3. 更关注一些y比较大的值，但是它的代价是对异常点过于敏感。如果预测出的y很不合理，则它的误差比较大，从而对RMSE的值有很大的影响。

2.3. RMSE(均方根误差)

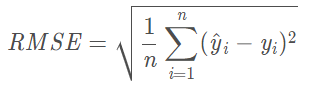
在MSE上加了根号，误差的结果和数据是一个级别，在数量级上更直观，如果RMSE=10，可以认为回归问题效果与真实结果平均相差10。

  1. 范围在$[0,\infin]$
  2. RMSE把更大的注意力放在y更大的值上，只有更大的y值预测准确了，模型的效果才会好。

2.4. MAPE(平均绝对百分比误差)

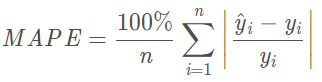
  1. 范围$[0,\infin]$，当MAPE=0%表示完美模型，MAPE大于100%表示劣质模型。
  2. 当真实值有数据等于0时，存在分母为0的情况，该公式不可用
  3. 比如将y1预测为1.5，和100预测为100.5，差值是一样的，。即1的MAPE比100的MAPE大很多。以MAPE作为loss函数时，更加关注y比较小的值。
  4. 单看MAPE的大小是没有意义的，因为MAPE是个相对值，而不是绝对值。MAPE只能用来对不同模型同一组数据的评估。比如对于同一组数据，模型A的MAPE比模型B小，可以说明模型A比模型B好。但是如果说MAPE=10%，并不能判断这个模型好还是不好

2.5. 总结

综上，在选用评价指标时，需要考虑

  1. 数据中是否有0，如果有0值就不能用MPE、MAPE之类的指标；

  2. 数据的分布如何，如果是长尾分布可以选择带对数变换的指标，中位数指标比平均数指标更好；

  3. 是否存在极端值，诸如MAE、MSE、RMSE之类容易受到极端值影响的指标就不要选用；

  4. 得到的指标是否依赖于量纲(即绝对度量，而不是相对度量)，如果指标依赖量纲那么不同模型之间可能因为量纲不同而无法比较；

3. 分类问题

在二分类任务中，使用Precison，Recall和F1值来评价分类的效果。

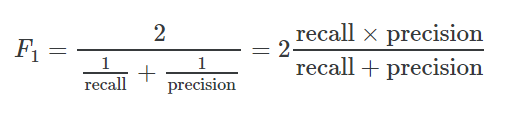
F1是针对二分类的，对于多分类，有2个常用的指标，Marco-F1和Micro-F1.

3.1. Micro-F1

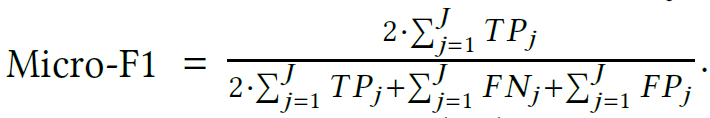
假设对于一个多分类问题，有三个类，分别是1，2，3

$TP_i$表示分类$i$的TP
$FP_i$表示分类$i$的FP
$TN_i$表示分类$i$的TN
$FN_i$表示分类$i$的FN
接下来，我们来计算Micro的Precison

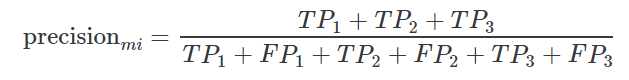
以及Micro的Recall

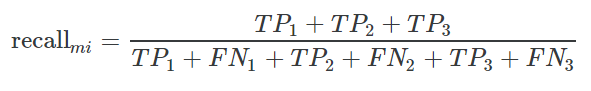
然后计算Micro-F1

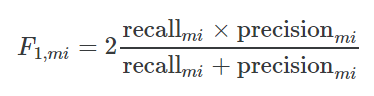
3.2. Macro-F1

先计算每个类的Precison和Rcall，从而计算出每个类的F1，然后将所有类的F1值平均得到Macro-F1。
如果数据集中各个类的分布不均衡的话，建议使用Micro-F1。
Macro-F1平等的看待各个类别，它的值更容易受少类别的影响Micro则更容易受常见类别的影响。

排序指标

AP(Average Precision)

推荐系统常见评测标准之MAP

当我们用Google搜索玫瑰的图片时，返回了10个结果，从最可能到最不可能排名，最好的情况是这10个结果都是我们想要的信息，但是如果只有部分信息是相关的，比如5个，那这5个结果如果排名靠前也是一个不错的结果，但是如果这5个相关结果排在6~10名，那这种情况下就比较差。这便是AP反映的指标，与recall类似，不过是“顺序敏感的recall”

【注】排名从1开始

例如：搜索玫瑰，返回10个图片，从最可能到最不可能排序。这10个图片的结果分别是：1,0,0,1,1,1,0,1,0,1，其中1表示是玫瑰，0表示不是。即搜索结果中，玫瑰图片的排名分别是[1,4,5,6,8,10]，AP=(1/1+2/4+3/5+4/6+5/8+6/10)/6=0.665

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def AP(ranked_list, ground_truth):
    """Compute the average precision (AP) of a list of ranked items

    """
    hits = 0
    sum_precs = 0
    for n in range(len(ranked_list)):
        if ranked_list[n] in ground_truth:
            hits += 1
            sum_precs += hits / (n + 1.0)#排名从1开始，因为n从0开始，所以加1
    if hits > 0:
        return sum_precs / len(ground_truth)
    else:
        return 0
打赏
0%