参考资料:
https://zhuanlan.zhihu.com/p/33006526
什么是梯度消失和梯度爆炸,分别会引发什么问题
1. 为什么使用梯度更新规则
现在,神经网络的参数都是通过反向传播更新的。深层神经网络由很多分线性层堆叠,每一个非线性层都可以看做是一个非线性函数。神经网络就是一个复合的非线性函数,将输入映射成输出。损失函数就是使关于真实值与预测值之间的误差。通过损失函数对参数求导,得到梯度,梯度的含义就是这个参数对整个网络的影响程度大小。使用梯度下降更新参数。
梯度决定了网络(参数)的学习速率。如果梯度出现异常,参数更新出现异常,即神经元失去了学习的能力。
如果权重的值都小于1,最终的输出很小,
如果权重的值都大于1,最终的输出很大,
- 在反向求导时,假设对$W^1$求梯度,如果其他的权重都小于1,求得的梯度很小,出现梯度消失,使用$W-\alpha \Delta W$,权重更新的很慢,训练的难度大大增加。梯度消失比梯度爆炸更常见
- 在反向求导时,如果权重大于1,梯度大幅度更新,网络变得很不稳定。较好的情况是网络无法利用训练数据学习,最差的情况是梯度或权重增大溢出,变成网络无法更新的Nan值。
不用层的参数更新速率不一样,一般靠近网络输出层的参数更新速度加快,学习的情况较好。靠近网络输入层的参数更新速度慢,学习的很慢,有时候训练了很久,前几层的权重参数值和刚开始初始化的值差不多。因此,梯度消失和爆炸的根本原因在于反向传播法则。
2. 激活函数
(1)在权重更新的时候,需要计算前层的偏导信息,因此如果激活函数选择的不合适,比如sigmoid,梯度消失的很明显。因为sigmoid的导数不会超过0.25,经过链式求导,很容易出现梯度消失。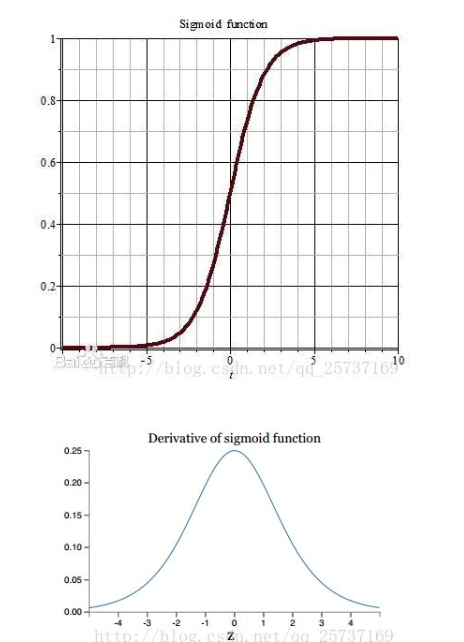
(2)tanh比sigmoid好一些,但是它的导数仍然小于1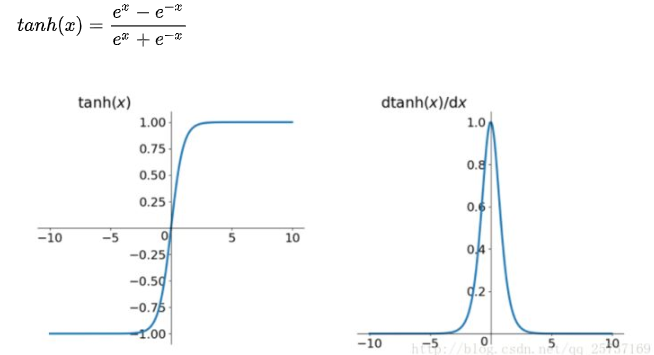
3. 初始化缓解梯度消失和爆炸
使用Xavier初始化:基本思想是通过网络层时,输出和输出的方差相同。Xavier在tanh中表现很好,但在Relu激活函数中表现很差。
何凯明提出了针对Relu的初始化方法
Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification He, K. et al. (2015)
该方法集合He initialization,简单思想是:在Relu网络中,假定每一层有一半的神经元被激活,另一半为0,所有,要保持方差不变,只需要在Xavier的基础上再除以2。
针对Relu的激活函数,基本使用He initialization。
- Xavier初始化:tanh,sigmoid激活函数
- He初始化:Relu激活函数
4. 如何判断出现梯度爆炸
当出现以下信号时,说明出现了梯度爆炸:
- 训练过程中,每个节点和层的权重梯度连续大于1
- 模型不稳定,梯度显著变化,快速变大
- 训练过程中,权重变成了Nan
- 权重无法从训练数据中更新
5. 如何解决梯度爆炸
- 梯度剪切
此方法针对梯度爆炸提出来的,基本思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过了这个阈值,就强制限制在这个范围之,这可以防止梯度爆炸。 - 权重正则化
比较常见的是L1正则化和L2正则化。正则化是通过对网络权重做正则化限制过拟合
Relu,LeakRelu激活函数
如果激活函数的导数为1,就不存在梯度爆炸的问题了。每层网络都可以得到相同的更新速度。在深层网络中使用relu激活函数不会导致梯度消失和爆炸的情况。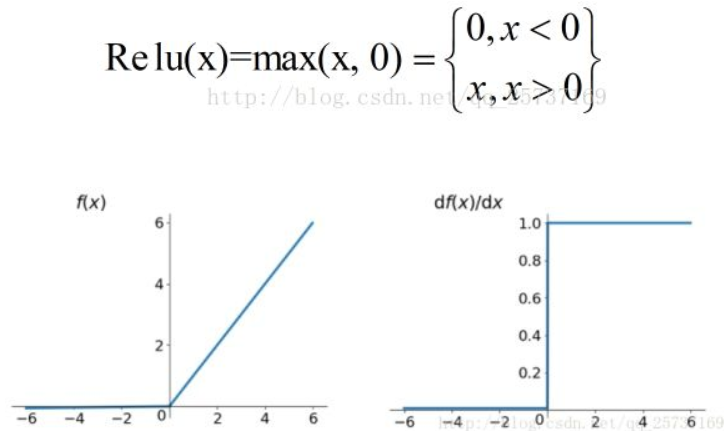
relu的主要贡献在于:
- 解决了梯度消失、爆炸的问题
- 计算方便,计算速度快
- 加速了网络的训练
同时也存在一些缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决);输出不是以0为中心的
- BatchNorm
- RestNet
- LSTM,可以解决梯度消失的问题

