1. 卷积
卷积操作需要有1一个数组和一个卷积核,假设卷积核的形状为pxq,代表卷积核的高和宽。二维卷积层的输入输出用4维表示,格式为(样本,通道,高,宽)
假设输入的形状为$n_h,n_w$,卷积核的形状为$k_hxk_w$,那么输出的形状为
卷积层的输出形状由输入形状和卷积核窗口形状决定,下面介绍卷积层的两个超参数,填充和步幅。
1.1. 填充
填充通常在输入的高和宽填充0元素,如果在高的两侧一共填充$p_h$行,在宽的两侧一共填充$p_w$列,那么输出形状为
1.2. 步幅
步幅表示卷积核一次移动的个数,当高的步幅为$s_h$,宽的步幅为$s_w$,输出形状为
1.3. 小结
- 填充可以增加输出的高和宽,常用来使输出与输入具有相同的高和宽
- 步幅可以减小输出的高和宽,使得输出的高和宽为输入的$1/n$
1.4. 通道channel
通道(channel):每个卷积层中卷积核的数量。这篇文章关于channel讲的很好
下面X(x_in,h,w)
K(k_out,k_in,h,w)
1 | X = nd.random.uniform(shape=(3, 3, 3)) |
1.5. 池化层
pooling层(池化层)的输入一般是上一个卷积层,主要有以下2个作用:
- 保留主要的特征,同时减少下一层的参数和计算量,防止过拟合
- 保持某种不变性,包括平移,旋转,常用的平均池化和最大池化
池化层的输出通道数和输入通道数相同
1.6. CNN应用
(1)2D卷积,输入和输出形状一样:一般kernel_size=(3,3),padding=1,stride=1,输入和输出的形状一样
(2)2D卷积,输入和输出高和宽减半:kernel_size=(3,3),padding=1,stride=2,输出的形状是输入一半
(3)3D卷积,一般kernel_size=(3,3,3),padding=1,stride=1,输入和输出的形状一样
(4)3D卷积,一般kernel_size=(1,1,1),padding=0,stride=1,输入和输出的形状一样
2. CNN五大经典模型
- Lenet:1986年
- Alexnet:2012年
- GoogleNet:2014年
- VGG:2014年
- Deep Residual Learning:2015年
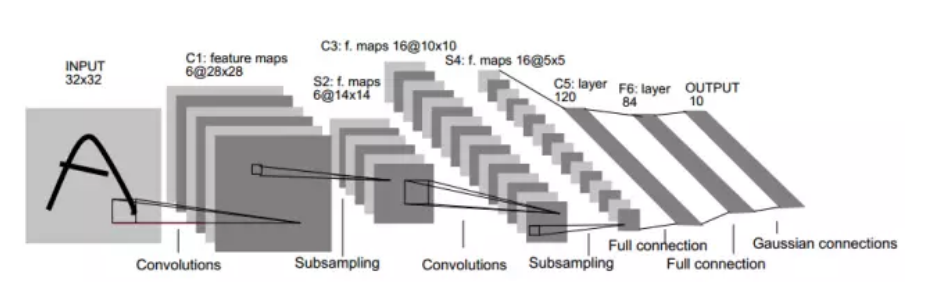
2.1. LeNet
LeNet交替使用卷积层和最大池化层后接全连接层进行图像分类。网络结构如下所示
2.2. AlexNet
2012年,ImageNet比赛冠军的model—AlexNet,以第一作者alex命名。这个model的意义比后面的那些model都大很多。首先它证明了CNN在复杂模型下的有效性,然后GPU实现使得训练在可接受的时间范围内得到结果,让CNN和GPU都火了一把。
AlexNet包含8层变换,其中5层卷积和2层全连接层隐藏层,1个全连接输出层。
AlexNet将sigmoid激活函数改成了简单的ReLu激活函数。一方面,ReLu激活函数更简单,例如它没有sigmoid激活函数中的求幂运算。另一方面,ReLu激活函数在不同的参数初始化方法下使得模型更容易训练。这是由于当sigmoid激活函数输出极接近0或1时,这些区域的梯度为0,从而造成反向传播无法继续更新部分模型参数;而ReLu激活函数在正区间的梯度恒为1.因为,若模型参数初始化不当,sigmoid函数可能在正区间得到几乎为0的梯度,从而令模型无法得到有效训练。
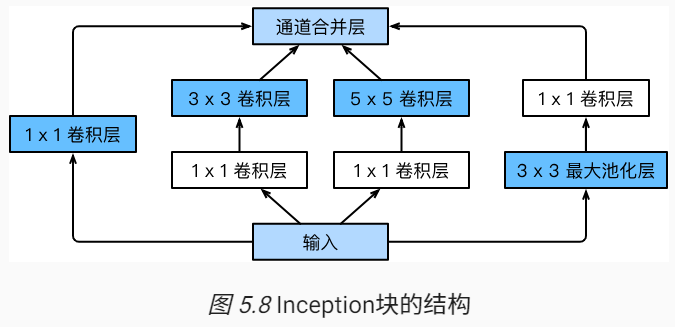
2.3. GoogleNet
2014年的ImageNet图像s识别挑战赛的冠军。
GoogleNet中的基础卷积块叫做Inception块。
2.4. VGG
VGG卷积块的组成规律是:连续使用数个相同的填充为1,窗口形状为3x3的卷积层后接一个步幅为2,窗口形状为2x2的最大池化层。卷积层保持输入的高和宽不变,而池化层则对其减半。
VGG网络=VGG卷积块+n个全连接层
VGG卷积块=n个相同的卷积层+1个最大池化层
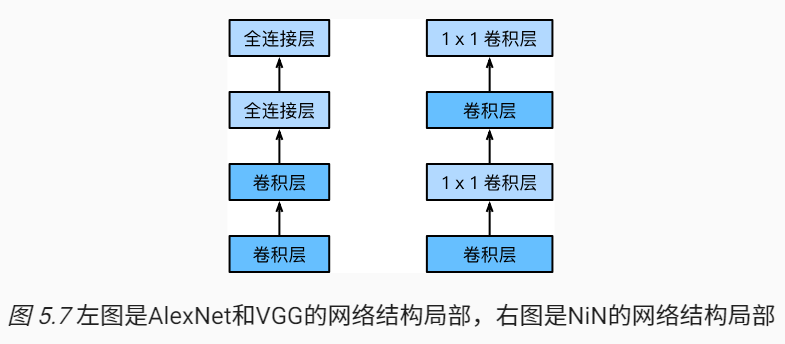
2.5. NiN
前面介绍的LeNet、AlexNet和VGG在设计上的共同之处是:先以卷积层构成的模块充分抽取空间特征,再以全连接层构成的模块来输出分类结果。其中AlexNet和VGG对LeNet的改进主要在于如何对这两个模块加宽(增加通道数)和加深。本节介绍网络中的网络(NiN),即串联多个由卷积层和全连接层构成的 小网络来构建一个深层网络。
解决深度为
全连接层可以由1x1卷积层充当
NiN块是NiN中的基本块。它由一个卷积层加两个充当全连接层的1x1卷积层串联而成。其中第一个卷积层的超参数可以自行设置,而第二个和第三个卷积层的超参数一般是固定的。
2.6. 批量归一化层
标准化处理:处理后的任意一个特征在数据集中所有样本上的均值为0,标准差为1.标准化处理输入数据使各个特征的分布相近:这样往往更容易训练处有效的模型。
通常来说,数据标准化预处理对于浅层模型就足够有效了。随着模型训练的进行,当每层中参数更新时,靠近输出层的输出较难出现剧烈变化但对深层神经网络来说,即使输入数据已经做了标准化,训练中模型参数的更新依然很容易造成靠近输出层的输出剧烈变化。这种计算数值的不稳定性通常令我们难以训练处有效的深度模型。
标准归一化的提出正是为了应对深度模型训练的挑战。在模型训练时,批量归一化利用小批量上的均值和标准差,不断调整神经网络中间输出,从而使整个神经网络在各层的中间输出的数值更稳定。BatchNorm主要是让训练收敛更快。
对全连接层和卷积层做批量归一化的方法不同。
- 对全连接层做批量归一化
权重参数和偏差参数分别为$W和b$,激活函数为$\phi$,批量归一化运算符为$BN$,使用批量归一化的全连接层的输出为
- 对卷积层做批量归一化
对卷积层来说,批量归一化发生在卷积计算之后,应用激活函数之前.
对于前面的模型,我们可以在卷积层或全连接层之后、激活层之前加入批量归一化层,以LeNet为例: - 未加入批量归一化层
1 | net=nn.Sequential() |
- 加入批量归一化层
在卷积层或全连接层之后,激活层之前加入批量归一化层
1 | net = nn.Sequential() |
2.7. 残差网络ResNet
2015年ImageNet冠军model。
深度网络的好处:特征的等级随着网络深度的加深二变高,及其深的深度使得该网络拥有强大的表达能力。
但不是网络层数越多,效果就越好。随着网络深度的加深,(1)会出现梯度衰减的问题,在反向传播时,使梯度不断下降直至消失,对于权重的更新会越来越慢,直至不更新。(2)并且较深层网络比较浅的网络有更高的训练误差,称为退化问题。
深度残差网络主要思想很简单,就是在标准的前馈卷积网络上,加一个跳跃绕过一些层的连接。每绕过一层就产生一个残差块(residual block),卷积层预测加输入张量的残差。普通的深度前馈网络难以优化。除了深度,所加层也使得training和validation的错误率增加,即使用上了batch normalization也是如此。残差神经网络由于存在shorcut connections,网络间的数据流通更为顺畅。残差网络结构的解决方案是,增加卷积层输出求和的捷径连接。
实验表明,残差网络更容易优化,并且能够通过增加相当的深度来提高准确率。核心是解决了增加深度带来的副作用(退化问题),这样能够通过单纯地增加网络深度,来提高网络性能。
- 网络的深度为什么重要?
因为CNN能够提取low/mid/high-level的特征,网络的层数越多,意味着能够提取到不同level的特征越丰富。并且,越深的网络提取的特征越抽象,越具有语义信息。 为什么不能简单地增加网络层数?
对于原来的网络,如果简单地增加深度,会导致梯度弥散或梯度爆炸。
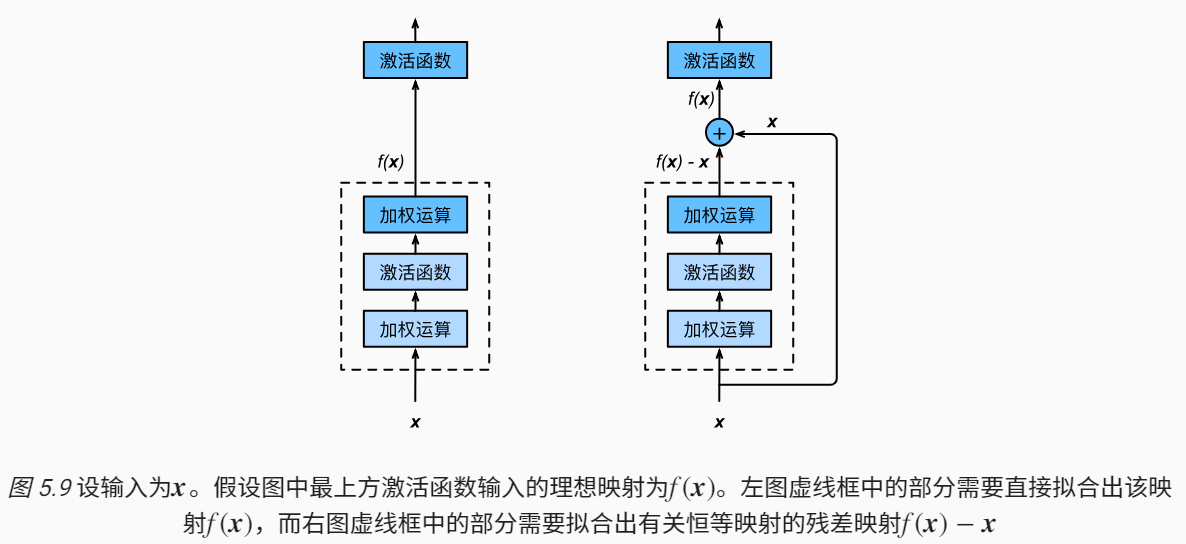
对于该问题的解决方法是正则化初始化和中间的正则化层(Batch Normalization),这样的话可以训练几十层的网络。虽然通过上述方法能够训练了,但是又会出现另一个问题,就是退化问题,网络层数增加,但是在训练集上的准确率却饱和甚至下降了。这个不能解释为overfitting,因为overfit应该表现为在训练集上表现更好才对。退化问题说明了深度网络不能很简单地被很好地优化。 作者通过实验:通过浅层网络+ y=x 等同映射构造深层模型,结果深层模型并没有比浅层网络有等同或更低的错误率,推断退化问题可能是因为深层的网络并不是那么好训练,也就是求解器很难去利用多层网络拟合同等函数。怎么解决退化问题?
深度残差网络。如果深层网络的后面那些层是恒等映射,那么模型就退化为一个浅层网络。那现在要解决的就是学习恒等映射函数了。但是直接让一些层去拟合一个潜在的恒等映射函数H(x) = x,比较困难,这可能就是深层网络难以训练的原因。但是,如果把网络设计为H(x) = F(x) + x。我们可以转换为学习一个残差函数F(x) = H(x) - x. 只要F(x)=0,就构成了一个恒等映射H(x) = x. 而且,拟合残差肯定更加容易。
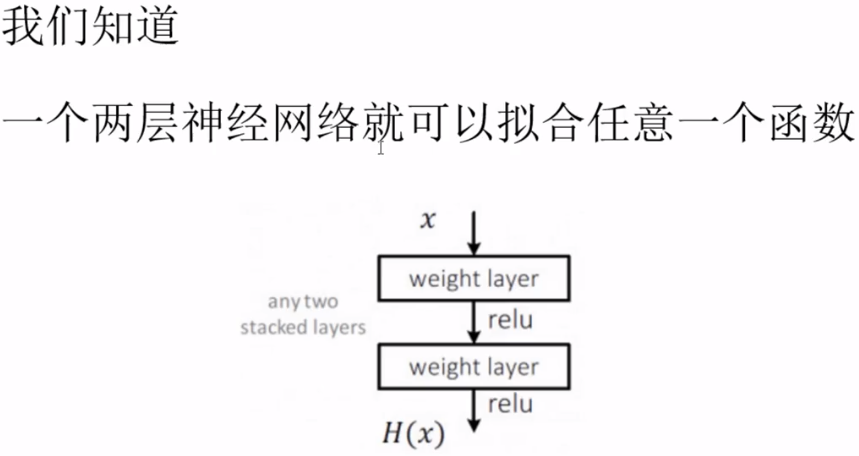
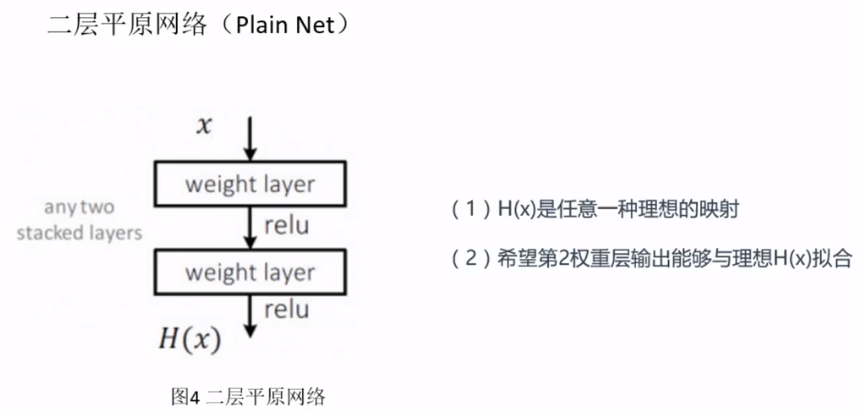
二层平原网络我们根据输入$x$,去拟合$H(x)$,$H(x)$是任意一种理想的映射,希望第2层权重输出能够与理想$H(x)$拟合。
为了解决深度神经网络的2个问题,提出残差网络ResNet。
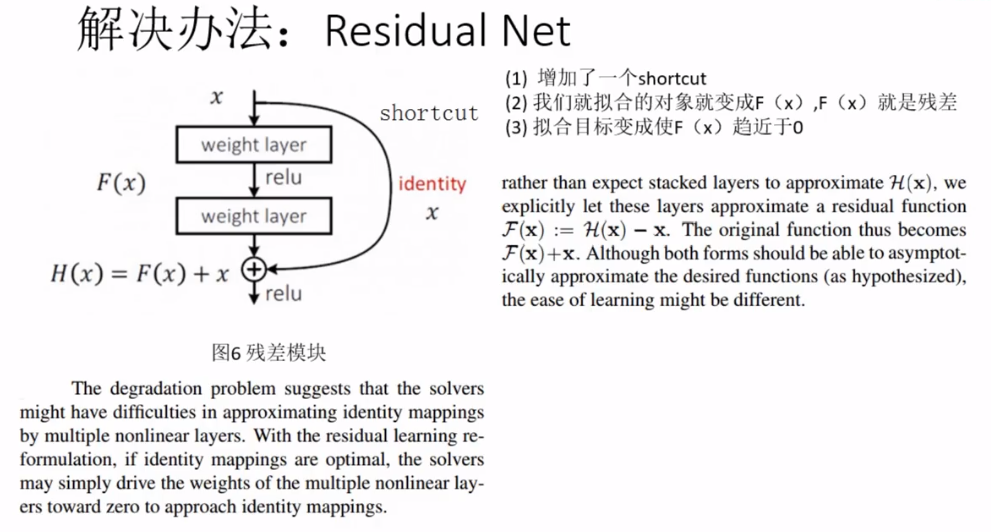
残差是$F(X)$,让$F(x)=0$,这样$H(X)就趋近于x,是一个恒等映射$,输出和输入相等,这样计算增加网络深度,也不会造成训练误差上升(退化问题)。


残差网络的基础块是残差块,在残差块中,输入可通过跨层的数据线路更快地向前传播。