以前看了一些《动手学深度学习》的教程,但是没有看完,寒假在家觉得时间还多,所以把以前看过的内容再看一遍,下面是第二次看的一些收获,记录下来,以备后需。
- 1. Softmax回归
- 2. Sigmoid和Softmax
- 3. 交叉熵损失函数
- 4. 优化算法
- 5. batch size
- 6. 使用gluon定义模型
- 7. 过拟合和欠拟合
- 8. 模型参数初始化
- 9. GPU计算
- 10. Block
- 11. 混合编程
- 12. 疑惑
- 13. 偏置
- 14. 模型参数
- 15. 自定义层
1. Softmax回归
- Softmax回归是用来分类的,输入的个数表示特征,输出的个数表示类别。
- Softmax运算
其中
softmax运算是把数据归一化到(0,1)之间。Softmax回归中有Softmax运算才可以使得输出的结果相加为1。如果没有softmax运算,输出结果也是可以用来分类的,例如$y_1=0.1$,$y_2=10$,$y_3=0.1$,最终属于的类别是2。但是如果$y_1=100$,$y_2=10$,$y_3=0.1$,最终属于的类别是1,没有经过softmax运算,会使得输出层的输出值的范围不确定,难以直观判断这些值的意义。
2. Sigmoid和Softmax
sigmoid通常用于二分类,不用于多分类。现在的深度学习模型多分类最后一层都是softmax。Softmax是把一个向量映射成另一个向量,这个向量中每个值在0~1之间,且元素之和为1。sigmoid作为最后一层输出一个值,这个值在(0,1)之间,表示属于正例(一类)的概率。softmax会输出n个值,这n个值在(0,1)之间,表示属于n个类的概率。
3. 交叉熵损失函数
对于2分类来说,模型最后通常会经过一个sigmoid函数,真实的标签是[0,1],sigmoid函数会输出一个概率值,这个概率值反映了这个样本属于正类1的概率,在(0,1)之间。分类问题的准确性通过交叉熵损失函数来判定。单个样本的交叉熵损失函数的公式:
如果是计算N个样本总的损失函数,只要将N个loss叠加就可以了:
交叉熵损失函数可以表示真实样本标签和预测标签之间的差值。先看一个样本的交叉熵损失函数,当真实标签$y=1$时,$L = -log\hat{y}$ ,这时,损失L与预测输出的关系如下:
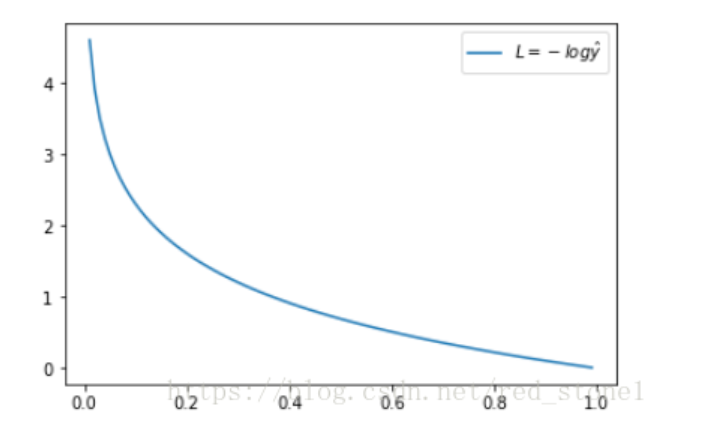
横坐标是预测输出,纵坐标是误差。当预测输出越接近1,损失函数L越小,预测输出越接近0,L越大。因此函数的变化趋势完全符合实际需要的情况。L表示预测输出与真实y的差距。模型输出的$\hat{y}$反映了这个样本属于正例的概率,当输出为1时,说明这个样本属于正例的概率为1,即预测为正例,L=0。预测出样本属于正例的概率越大,L越小。
在多分类中,使用softmax作为最后的输出层,输出的是一个向量,经过softmax运算会得到这个样本属于n个类的概率,在计算交叉熵时,需要用到这个概率向量。一个样本真实的分类结果可以用一个向量来表示,其中只有一个是1,其余全为0。第i个样本真实的向量为$\boldsymbol{y}^{(i)}$,预测的向量为$\boldsymbol{\hat{y}^{(i)}}$
交叉熵用来评估预测值和真实值之间的差异
向量$\boldsymbol{}y^{(i)}$中共有q个元素,其中只有一个元素为1,其余全部为0,于是$H\left(\boldsymbol{y}^{(i)},\boldsymbol{\hat{y}^{(i)}}\right)=-\log\hat{y}_j^{(i)}$,交叉熵只关心正确类别的预测概率,比如样本$i$的真实类别为5,那么只关心预测向量$\hat{y}^{(i)}$中的第5个元素,即样本$i$属于第5个类别的概率。
假设训练数据集的样本个数为$n$,交叉熵损失函数定义为
其中$\Theta$代表模型参数,对于这$n$个样本,每一个样本都求出这个样本的交叉熵。如果是一个样本只属于一个类,那么向量$\boldsymbol{}y^{(i)}$中只有1个为1,其余全为0。交叉熵损失函数可以简写成$\ell(\boldsymbol{\Theta})=-\frac{1}{n}\sum_{i=1}^n\log\hat{y}_j^{(i)}$,若要交叉熵损失函数$\ell(\boldsymbol{\Theta})$最小,就要使$\sum_{i=1}^n\log\hat{y}_j^{(i)}$最大,即最大化$\prod_{i=1}^n\hat{y}_j^{(i)}$,即每个样本属于自己正确类别的联合概率。
3.1. softmax运算步骤
对于分类问题,输出的结果是$O$,$O$是一个矩阵,其中行数表示样本的个数,列数表示类别的个数,假设有100个样本,5类,$O$是一个100*5的矩阵。通过softmax运算使得一行的和为1,可以直观的看出每个样本属于每个样本的概率大小。
- 首先对矩阵的中每个元素做exp()运算
- 计算出每一行的sum()
然后用一行中的每个元素/该行的sum()
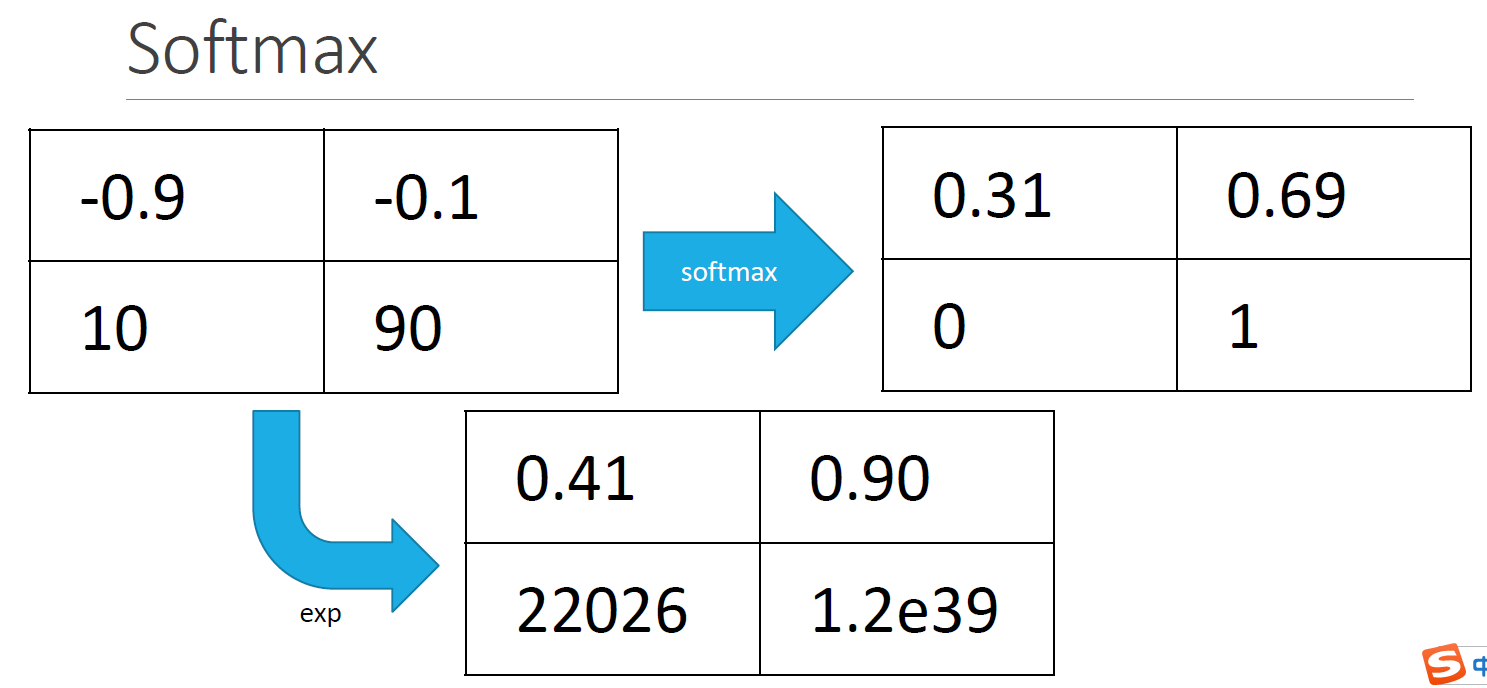
代码如下
1
2
3
4def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(axis=1, keepdims=True)
return X_exp / partition # 这里应用了广播机制
4. 优化算法
优化算法就是用来更新模型参数的一种算法,模型在训练的时候通过反向传播计算梯度,然后更新模型参数,使得模型的损失越来越小,当模型参数不再变化时,训练结束。
4.1. 梯度下降GD
一次迭代中更新一次模型参数,梯度下降在每一次迭代中,使用整个训练数据集来计算梯度,更新一次参数。一个epoch只有一次迭代,下一次epoch再次使用所有的训练数据集更新模型参数。
4.2. 随机梯度下降SGD
梯度下降每次更新模型参数时都需要遍历所有的data,当数据量太大或者一次无法获取全部数据时,这种方法并不可行。这个问题基本思路是:每次迭代只通过一个随机选取的数据$(x_n,y_n)$来获取梯度,以此对w进行更新,这种方法叫做随机梯度下降。一次迭代使用一个样本更新模型参数,这样一个epoch就需要很多次迭代,每次迭代随机采样一个样本更新模型参数。
小批量随机梯度下降中,当批量大小为1时是随机梯度下降;当批量大小为训练数据样本数时是梯度下降。当batch size较小时,每次迭代中使用的样本少,导致并行处理和内存使用效率变低。这使得在计算相同数据样本的情况下比使用更大batch size时所花的时间更多,即相同的训练数据,batch size越小,训练时间越长。当批量较大时,每个批量梯度里可能含有更多的冗余信息,为了得到较好的模型参数,批量较大时比批量较小时需要计算的样本数目可能更多,即迭代周期数多。
- 相同的训练数据,batch size较小比batch size大时需要的训练时间长。
- 相同的训练数据,batch size大时,为了达到和batch size小时一样的训练效果,需要的epoch多。
4.3. 小批量随机梯度下降
小批量随机梯度下降:在每次迭代中,随机均匀采样多个样本组成一个小批量,然后使用这个小批量来计算梯度,更新模型参数。
小批量随机梯度下降的学习率可以在迭代中自我衰减
4.4. 学习率
当学习率很小时,模型参数更新非常慢,训练时间会很长。当学习率很大时,模型可能会越过最优解,导致模型不收敛,训练误差会越来越大,出现nan。当loss出现nan的时候,可以减少学习率。
5. batch size
梯度下降是用来寻找模型最佳的模型参数w和b的迭代优化算法,通过最小化损失函数(线性回归的平方差误差、softmax的交叉熵损失函数),来寻找w和b。
只有在数据量比较大的时候,才会用到epoch和batch size和迭代,但这3个词代表什么意思呢?一直不太清楚
- epoch:当一个完整的数据集通过了神经网络一次并且返回了一次,这个过程称为一个epoch。
- batch size:当一个完整数据集太大时,不能一次将全部数据输入到神经网络中进行训练,所以需要将完整数据集进行分块,每块样本的个数就是batch size。batch size是为了在内存效率和内存容量之间寻找最佳平衡。
- 迭代:就是以batch size向神经网络中输入样本,将完整数据集输入到神经网络中所需的次数,即完成一次epoch的次数。迭代数=batch的个数。比如完整数据集2000个样本,每个batch有200个样本,那么共有10个batch,完成一个epoch需要10次迭代。
在读取数据的时候传入一个参数batch_size,这个函数返回的X和y分别是含有batch_size个样本的特征和标签。
1 | for X, y in data_iter(batch_size, features, labels): |
在进行小批量随机梯度算法中,一个batch size更新一次梯度,如果完整训练集中有2000个样本,一个batch有200个样本,那么一次epoch中更新10次模型参数。
1 | def sgd(params, lr, batch_size): |
1 | lr = 0.03 |
5.1. 总结
CIFAR10 数据集有 50000 张训练图片,10000 张测试图片。现在选择 Batch Size = 500 对模型进行训练.
- 每个epoch要训练的图片数量:50000
- 训练集中具有的batch个数:50000/500=100
- 每次epoch需要的batch个数:100
- 每次epoch需要的迭代(iteration)个数:100
- 每次epoch中更新模型参数的次数:100
- 如果有10个epoch,模型参数更新的次数为:100*10=1000
- 一次epoch使用的是全部的训练集50000中图片,下一次epoch中使用的还是这50000张图片,但是对模型参数的权重更新值却是不一样的,因为不同epoch的的模型参数不一样,模型训练的次数越多,损失函数越小,越接近谷底。
- 适当增加batch size的优点:
(1)提高内存利用率
(2)一次epoch的迭代次数减少,相同数据量的处理速度更快,但是达到相同精度所需的epoch越多
(3)梯度下降方向准确度增加,训练震荡越小 - 减少batch size的缺点
(1)小的batch size引入的随机性越大,难以达到收敛
6. 使用gluon定义模型
在gluon中无须指定每一层输入的形状,例如线性回归的输入个数,当模型得到数据时,例如执行后面的net(X)时,模型将自动推断出每一层的输入个数
6.1. 线性回归
1 | #先导入nn模块 |
6.2. softmax回归
1 | %matplotlib inline |
6.3. 多层感知机
输入层、隐藏层256个节点,输出层10个节点,relu激活函数
1 | net = nn.Sequential() |
7. 过拟合和欠拟合
7.1. 验证数据集
测试数据集只能在所有超参数和模型参数都选定后使用一次。不可以使用测试数据集选择模型参数。所以需要验证集用来选择模型,验证集不参会模型训练。
7.2. 权重衰减
权重衰减等于L2范数正则化,用来减少过拟合
7.3. 丢弃法
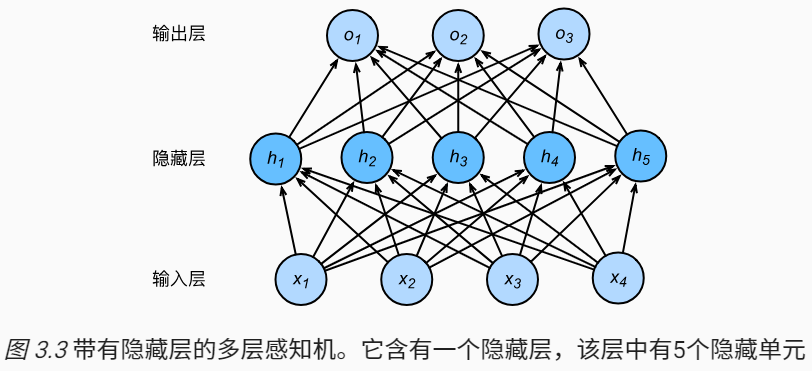
深度学习模型常常使用丢弃法(dropout)来应对过拟合。在训练过程中,对隐藏层使用丢弃法,这样隐藏层中的某些神经元将会为0,即被丢弃。下图是一个多层感知机,隐藏层有5个神经元。
其中
隐藏层计算的结果$h_i$将以$p$的概率被丢弃,即$h_i=0$,丢弃概率$0<=p<=1$。由于在训练中隐藏层神经元的丢弃是随机的,即$h_1$…$h_5$中的任一个都有可能被清零,输出层的计算无法过度依赖隐藏层$h_1$…$h_5$中的任一个,从而在训练模型时起到正则化的作用,用来应对过拟合。在测试模型时,为了拿到更加确定的结果,一般不使用丢弃法。
假设$h_2=0,h_5=0$,使用丢弃法之后的模型为
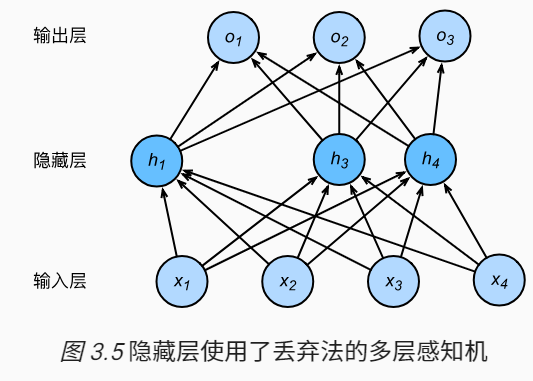
代码实现
在Gluon中,只需要在全连接层后面添加Dropout层并指定丢弃概率。在训练模型时,Dropout将以指定的丢失概率随机丢弃上一层的输出元素;在测试模型时,Dropout不起作用。
一般在靠近输入层的丢弃率较小
1 | net = nn.Sequential() |
8. 模型参数初始化
8.1. 随机初始化
在Mxnet中,随机初始化通过net.initialize(init.Normal(sigma=0.01))对模型的权重参数w采用正太分布的随机初始化。如果不指定初始化方法,如net.initialize(),默认的初始化方法:权重参数w每个元素随机采样于-0.07到0.07之间的均匀分布,偏差b为0。
8.2. Xavier随机初始化
假设某全连接层的输入个数为$a$,输出个数为$b$,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
8.3. 模型参数的延后初始化
模型net在调用初始化函数 initialize之后,在做前向计算net(X)之前,权重参数的形状出现了0.

在之前使用gluon创建的全连接层都没有指定输入个数,例如使用感知机net里,创建的隐藏层仅仅指定输出大小为256,当调用initialize函数时,由于隐藏层输入个数依然未知,系统无法知道隐藏层权重参数的形状,只有在当我们将形状为(2,20)的输入X传进网络进行前向计算net(X)时,系统才推断该层的权重参数形状为(256,20),因此,这时候才真正开始初始化参数.
9. GPU计算
使用GPU进行计算,通过ctx指定,NDArray存在内存上,在创建NDArray时可以通过指定ctx在指定的gpu上创建数组
1 | a=nd.array([1,2,3],ctx=mx.gpu()) |
同NDArray类似,Gluon的模型也可以在初始化时通过ctx参数指定设备,下面的代码将模型参数初始化在显存上。当输入x是显存上的NDArray时,gluon会在同一块显卡的显存上计算结果。
mxnet要求计算的所有输入数据都在内存或同一块显卡的显存上
1 | net=nn.Sequential() |
10. Block
上面使用Sequential来构造模型,下面介绍另一种方法:使用Block类来构造模型,它让模型的构造更加灵活。
Bolck类是nn模块里提供的一个模型构造类,我们可以继承它来构造我们想要的模型。下面继承Block类构造MLP,需要重载Block类的init函数和forward函数。
1 | from mxnet import nd |
1 | X = nd.random.uniform(shape=(2, 20)) |
首先需要实例化MLP,得到一个对象net,初始化net并传入X做一次前向计算。net(X)会调用MLP继承自Block类的call函数,这个函数会自动调用forward函数完成前向计算。
10.1. Sequential和Block的关系
Block类是一个通用的部件,Sequential类也继承了Block。Sequential类可以定义一些简单的模型,且不需要定义forward函数,但是直接继承Block类可以极大的拓展模型构造的灵活性。
10.2. 使用Block自定义层
虽然Gluon提供了大量常用的层,但是有时候还需要自定义的层。下面介绍如何使用NDArray来自定义一个Gluon层,从而可以重复调用。
10.3. 不含模型参数的自定义层
下面的CenteredLayer类通过继承Block类自顶一个将输入减掉均值后输出的层,并将层的计算定义在forward函数中。这个层只做了减法,所以不需要模型参数
1 | from mxnet import gluon,nd |
10.4. 含模型参数的自定义层
我们还可以自定义含模型参数的自定义层。其中的模型参数可以通过训练学到。在使用自定义层时,定义了模型参数,这时只是定义了参数的形状,并不会给参数初始化,参数初始化还是使用net.initialize()函数在自定义含模型参数的层时,我们可以利用Block类自带的ParameterDict类型的成员变量params。它是一个由字符串类型的参数名字映射到Parameter类型的模型参数的字典。我们可以通过get函数从ParameterDict创建Parameter实例。下面实现一个含参数权重和偏差参数的全连接层,使用ReLU函数作为激活函数,其中in_units表示输入的个数,units表示输出的个数。
1 | class MyDense(nn.Block): |
总结:使用nn.Block自定义层,在自定层中的init()方法中,自定义模型参数,使用self.params.get(‘参数名称’,shape=(a,b))。还可以自定义层,这个层中没有参数,我们在层中添加gluon.nn中的层,比如self.conv1 = nn.Conv2D()。初始化完之后,定义forward函数。在这个层定义好之后,需要创建一个网络对象,使用net=Sequential(),然后再net.add()添加需要的层,
11. 混合编程
使用HybridBlock类和HybridSequential类构建模型。默认情况下,它们和Block类或者Sequential类一样依据命令式编程的方式执行。当我们调用hybridize函数后,Gluon会转换成依据符号式编程的方式执行。事实上,绝大多数模型都可以接受这样的混合式编程的执行方式。
通过调用hybridize函数来编译和优化HybridSequential实例中串联的层的计算。模型的计算结果不变。
只有继承HybridBlock类的层才会被优化计算。例如,HybridSequential类和Gluon提供的Dense类都是HybridBlock类的子类,它们都会被优化计算。如果一个层只是继承自Block类而不是HybridBlock类,那么它将不会被优化。
11.1. 使用HybridSequential类构造模型
我们之前学习使用Sequential来串联多个层,为了使用混合式编程,将Sequential换成HybridSequential类
1 | from mxnet import nd,sym |
11.2. 使用HybridBlock自定义模型
和Sequential类与Block类之间的关系一样,HybridSequential类是HybridBlock类的子类。与Block实例需要实现forward函数不太一样的是,对于HybridBlock实例,我们需要实现hybrid_forward函数。
1 | class HybridNet(nn.HybridBlock): |
在继承HybridBlock类时,我们需要在hybrid_forward函数中添加额外的输入F。我们知道,MXNet既有基于命令式编程的NDArray类,又有基于符号式编程的Symbol类。由于这两个类的函数基本一致,MXNet会根据输入来决定F使用NDArray或Symbol
12. 疑惑
Dense(5),其中的5表示这一层输出的个数,Gluon中不需要指定每一层输入的形状,net(X)做的操作就是wx+b,只要把输入传进去,内部会自动进行前向计算,不需要传入w和b。
12.1. BN
参考资料
https://www.jiqizhixin.com/articles/2018-08-29-7
https://icml.cc/2016/tutorials/icml2016_tutorial_deep_residual_networks_kaiminghe.pdf
批量归一化层,不断调整神经网络的中间输出,从而使得整个神经网络在各层输出的中间值更稳定,主要是让收敛变快,加速训练,,对准确率影响不大
BN层的作用:
- 加快模型训练速度,更快收敛
- 允许使用更大的学习率,提高训练速度
可以选择比较大的初始学习率, - 减少对初始化的依赖,对参数初始化不敏感
提升训练稳定性 BN引入的噪声能够起到对模型参数进行正则化的作用,有利于增强模型泛化能力
BN的局限:Batchsize太小效果不佳
BN是严重依赖Mini-Batch中的训练实例的,如果Batch Size比较小,则效果有明显的下降。之所以这样,是因为小的BatchSize意味着数据样本少,因为得不到有效统计量,也就是说噪声太大。- BN在MLP和CNN上效果很好,但是在
RNN等动态网络上效果不明显.
对于RNN来说,尽管其结构看上去是个静态网络,但在实际运行展开时是个动态网络结构,因为输入的Sequence序列是不定长的,也就是说一个Mini-Batch中的训练实例又长又短。对于类似RNN这种动态网络结构,BN使用起来不方便
13. 偏置
原先一直以为卷积操作计算时不涉及偏置,后来发现卷积也涉及到偏置。 二维卷积层将输入和卷积核做卷积运算,并加上一个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差,在训练的过程中,通常我们先对卷积核随机初始化,然后不断迭代卷积核和偏差。
1 | class Conv2D(nn.Block): |
14. 模型参数
在定义好模型之后,使用initialize()对模型所有的参数进行初始化。在自定义层的时候,如果自定义层含有参数,这时候只需要对模型的参数指定名称(为了以后容易区分)和形状(不是必须的,如果是用参数延后初始化,可以不指定),一般不对参数指定初始化方式。使用initialize()对模型中的所有参数进行初始化,使用同一种初始化方式。
15. 自定义层
在自定义含有参数的层时,需要重写2个函数:init(),forward()。这2个函数中如果需要参数可以传入相应的参数。在init中主要是定义权重和偏差等,在forward中定义前向计算。实例化一个自定义层时传入的参数是init中的参数,比如gcn1 = gcn_layer(256),其中256是init的参数,然后前向计算时,传入的参数是forward的参数,gcn1(x)

